
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
|
|
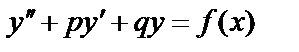 (3) – неоднородные линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
(3) – неоднородные линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
Теорема. Общее решение неоднородного уравнения (3) имеет вид

где  - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения  ,
, 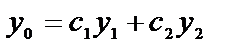 , где
, где  - произвольные постоянные,
- произвольные постоянные,  - какое – нибудь частное решение неоднородного уравнения (3).
- какое – нибудь частное решение неоднородного уравнения (3).
Частное решение  определяется в зависимости от вида правой части
определяется в зависимости от вида правой части  уравнения и характера корней характеристического уравнения согласно правилу, изложенному в следующей таблице:
уравнения и характера корней характеристического уравнения согласно правилу, изложенному в следующей таблице:
Замечание:
1) Многочлены  ;
; 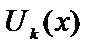 ;
;  должны быть полными, содержать все степени х.
должны быть полными, содержать все степени х.
2) Вид частного решения сохраняется и в том случае если, правая часть имеет неполный вид, например,  ,
,  и т.д.
и т.д.
3) Неизвестные постоянные А, В, С, …. Находят методом неопределенных коэффициентов.
4) Случай 1 следует из случай2 при 
5) Случаи 4 является частным случаем3 при  ,
,  ,
, 
| № | Вид правой части 
| Корни характеристического уравнения | Вид частного решения 
| ||
| 1 |  - многочлен степени n - многочлен степени n
| 1)0 не является корнем; 2) 0 является простым корнем; 3)0 является двукратным корнем. | 1)  многочлен степени n
2) многочлен степени n
2)  3)
3) 
| ||
| 2 | 
| 1)  - не является корнем;
2) - не является корнем;
2) 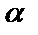 - простой корень;
3) - простой корень;
3) 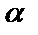 - двукратный корень. - двукратный корень.
| 1)  2)
2)  3)
3) 
| ||
| 3 | 
| 1) число  не является корнем;
2) число не является корнем;
2) число  является корнем. является корнем.
| 1) 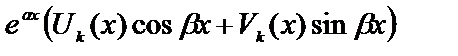 где где  ,
2) ,
2) 
| ||
| 4 | 
| 1) 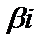 не является корнем;
2) не является корнем;
2)  является корнем является корнем
| 1) 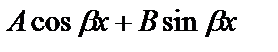 2)
2) 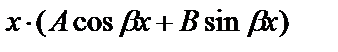
| ||
Пример1.  ,
, 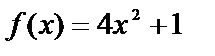 ,
,  ,
, 
1. 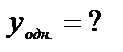
 ,
,  ,
, 
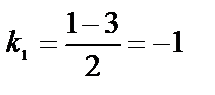 ,
, 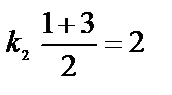 ,
, 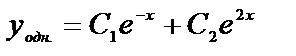
2. 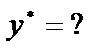 0 - не является корнем характеристического уравнения.
0 - не является корнем характеристического уравнения.
 , А, В, С=?
, А, В, С=?
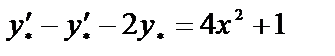 ,
,  ,
, 



 ,
, 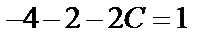 ,
, 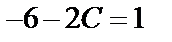 ,
, 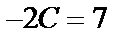 ,
, 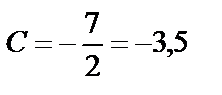
 ,
,  - частное решение
- частное решение

Вопросы для самопроверки
1. Дайте определение дифференциального уравнения.
2. Дайте определение уравнения с разделяющимися переменными.
3. Что называется общим решением дифференциального уравнения первого порядка?
4. Какое уравнение первого порядка называется однородным? Как оно решается?
5. Какое уравнение первого порядка называется линейным? Изложить способ его решения.
6. Что называется дифференциальным уравнением второго порядка?
7. Что называется линейным дифференциальным уравнением второго порядка?
8. Описать способ решения линейного уравнения второго с постоянными коэффициентами?
9. Какое уравнение называется характеристическим? Как оно составляется?
10. Указать вид решения в случае комплексных корней характеристического уравнения.
Рекомендуемая литература: ОЛ[2], [3], [4], [7],
 КРАТНЫЕ ИНТЕГРАЛЫ
КРАТНЫЕ ИНТЕГРАЛЫ
|
|