Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача 6.

Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если она станет двигаться в горизонтальном направлении с ускорением а₀= 1, 00 м/с². Длина плоскости l = 1, 0 м, угол наклона к горизонту a=30°, коэффициент трения между телом и плоскостью m = 0, 60.

Решение. Выберем систему отсчета, связанную с наклонной плоскостью. Пока плоскость покоится, на тело действуют три силы: сила тяжести , сила нормального давления 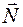опоры и сила трения покоя , которые уравновешивают друг друга. Как только начнется ускоренное движение плоскости и связанная с ней система отсчета станет неинерциальной, появится четвертая сила, действующая на тело, –сила инерции . Равновесие нарушится и тело начнет скользить вниз по наклонной плоскости с ускорением . Так как искомое время определяется известной формулой, связывающей время и перемещение, при равноускоренном движении без начальной скорости:

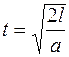, (1)

то надо найти ускорение a. Для этого запишем второй закон Ньютона в нашей неинерциальной системе отсчета:

(2)

Направим оси координат, как показано на рисунке. Проектируя все векторы, входящие в уравнение (2), на оси x и y, получим соответственно два скалярных уравнения:

(3)

(4)

Решив систему (3), (4) с учетом , найдем ускорение:

.

Теперь по формуле (1) имеем

.

Подставив числовые значения величин, найдем

.

Задача 7.

Собственное время жизни нестабильной элементарной частицы мюона равно 2.2мкс. Определить время жизни мюона в системе отсчета, где до распада он успевает пройти 20 км.

Решение.

Для решения этой задачи проще всего воспользоваться инвариантностью интервала между событиями.

В системе отсчета К, где мюон покоится, интервал Δ S между его рождением и распадом равен , где Dt –собственное время жизни частицы.

В системе отсчета К¢, где мюон успевает пройти до распада 20км, интервал Δ S^΄ между его рождением и распадом равен , где Dl¢ расстояние, разделяющее точки рождения и распада мюона в системе отсчета К¢.

Интервал между этими событиями остается постоянным при переходе от одной инерциальной системе к другой.

Следовательно: = .

Решая это уравнение получим: Dt¢ = = .

Следует отметить что полученный результат превосходит собственное время жизни в 30 раз!

Задача 8.

В дне цилиндрического сосуда имеется круглое отверстие диаметром 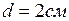. Диаметр сосуда . Найти зависимость скорости понижения уровня воды в сосуде от высоты этого уровня. Определить численное значение этой скорости для высоты .

Решение.

Рассмотрим состояние жидкости в верхнем сечении сосуда и в сечении отверстия. По формуле Бернулли:

или , (1)

где 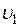- скорость течения воды в верхнем сечении (скорость понижения уровня воды в сосуде), - скорость вытекания воды из отверстия, p₀-атмосферное давление, h-высота верхнего уровня жидкости относительно отверстия. Вследствие несжимаемости жидкости: или , (2)

где - площадь поперечного сечения сосуда, - площадь поперечного сечения отверстия.

Подставляя (2) в (1) и решая относительно 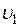, получим:

.

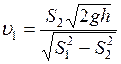Так как и , то .

Так как , то приближённо

. (3)

Подставив числовые значения в формулу (3), найдём:

м/с.

Задача 9.

Платформа, имеющая форму сплошного однородного диска, может свободно вращаться вокруг вертикальной оси. На краю платформы находится человек, масса которого в 4 раза меньше массы платформы. Найти отношение угловых скоростей вращения платформы в начальный момент и после того, как человек переместится в её центр. Человека рассматривать как материальную точку.

Решение.

Внешними силами в системе человек-платформа являются силы тяжести, направленные вертикально вниз. Проекция момента внешних сил на вертикальную ось, совпадающую с осью вращения платформы, равна нулю. Следовательно, момент импульса системы человек-платформа относительно оси вращения должен оставаться неизменным при перемещении человека относительно платформы:

I _сист ω = I^΄ _сист ω ^΄ ,

где: I _сист - момент инерции системы до изменения положения человека, I^΄ _сист - момент инерции системы после изменения положения человека, ω и ω ^΄ - угловые скорости системы соответственно до и после изменения положения человека. Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, следовательно, I _сист = I₁ + I₂, где I₁ – момент инерции платформы, I₂ – момент инерции человека.

Таким образом, I _сист = m₁ R² +m₂ R², где: m₁ и m₂ –массы платформы и человека, R – радиус платформы.

После того, как человек переместится в центр платформы, момент инерции платформы относительно оси вращения не изменится, а момент инерции человека обратится в нуль. С учетом этого получаем:

I^΄ _сист = m₁ R².

Таким образом, закон сохранения момента импульса системы можно представить в виде:

( m₁ R² +m₂ R²) ω = m₁ R² ω ^΄ .

Найдем отношение угловых скоростей системы до и после перемещения:

,

С учетом того, что m₁ =4 m₂, окончательно получим:

.