Решение. Будем считать, что в положении равновесия потенциальная энергия маятника равна нулю

Будем считать, что в положении равновесия потенциальная энергия маятника равна нулю. Тогда, с учетом того, что в верхнем положении маятника его кинетическая энергия должна быть минимальна и, следовательно, равна нулю, закон сохранения энергии примет вид:

, (1)

где - кинетическая энергия, сообщенная маятнику в положении равновесия, а - его потенциальная энергия в верхнем положении. Потенциальная энергия тела рассчитывается по формуле

, (2)

где - масса тела, а - высота его центра масс относительно нулевого уровня. В данном случае, за нулевой принят уровень, на котором находится центр масс маятника в положении равновесия

(точка С). В результате (см. рис.),

. (3)

Здесь, - координата центра масс маятника (ось направлена вниз, а ее начало находится на той же высоте, что и ось вращения маятника). Применим формулу для нахождения координаты центра масс составного тела

, (4)

в которой и соответственно масса и координата центра масс i^го тела. В нашем случае, ( - масса одного стержня). Соответственно, из формулы (3), , а с учетом формулы (2), потенциальная энергия маятника

. (5)

Теперь определим кинетическую энергию, сообщенную маятнику в положении равновесия. Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна

Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer

Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.

Что умеет делать SeoHammer

— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.

SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.

Зарегистрироваться и Начать продвижение

. (6)

Здесь - момент инерции тела относительно оси вращения, а - его угловая скорость. Момент инерции маятника , где и моменты инерции соответственно вертикального и горизонтального стержней относительно оси вращения. Известно, что момент инерции стержня относительно оси, проходящей через его конец, . Момент инерции горизонтального стержня найдем с помощью теоремы Штейнера: . В нашем случае, , а . Следовательно, .

Подставив данное выражение для момента инерции в (6), получим

. (7)

Подставив (5) и (7) в (1), получим

. Отсюда, .

Задача 5.

Однородный сплошной цилиндр массой 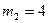кг может вращаться без трения вокруг оси. За эту ось, нерастяжимой невесомой нитью, перекинутой через блок массой кг, он привязан к бруску массой 1 кг. Определить ускорение цилиндра вдоль наклонной плоскости и силу трения, действующую на него, при качении без проскальзывания. Блок вращается без трения. Угол наклона плоскостей к горизонту . Коэффициент трения бруска о плоскость .

Решение:

На цилиндр действуют: сила тяжести , сила натяжения нити , сила реакции опоры и сила трения . Поскольку цилиндр катится без проскальзывания, то -- это сила трения покоя. Величина этой силы заранее неизвестна и находится в процессе решения (0 , где -- коэффициент трения). Силы, действующие на брусок, имеют тот же смысл и обозначены теми же буквами с индексом 1.

Сервис онлайн-записи на собственном Telegram-боте

Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.

Для новых пользователей первый месяц бесплатно.

Зарегистрироваться в сервисе

На блок действуют две силы натяжения и ( и ). Между собой они неравны (), так как в противном случае, результирующий вращающий момент, действующий на блок, равнялся бы нулю, и блок не вращался бы с ускорением.

Чтобы решить задачу, для цилиндра запишем второй закон Ньютона и уравнение динамики вращательного движения, для блока -- уравнение динамики вращательного движения, а для бруска -- второй закон Ньютона. Кроме того, будем использовать следующую связь между линейным ускорением центра масс цилиндра и его угловым ускорением , которая справедлива при качении без проскальзывания:

, (1)

где -- радиус цилиндра (в силу нерастяжимости нити, ускорения центров масс цилиндра и бруска одинаковы, то есть ). Если нить не проскальзывает относительно блока, то формула (1) также связывает его угловое ускорение с линейным ускорением центров масс бруска и цилиндра (В этом случае, в ней нужно заменить на радиус блока ).

Рассмотрим качение цилиндра. Второй закон Ньютона для него имеет

следующий вид:

. (2)

Спроектировав (2) на ось 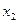, получим с учетом условия , что

. (3)

При записи уравнения динамики вращательного движения цилиндра относительно его оси симметрии, учтем, что моменты сил тяжести, реакции опоры и натяжения нити равны нулю (их плечи равны нулю). В результате, уравнение динамики вращательного движения примет следующий вид:

. (4)

Здесь -- радиус цилиндра,

(5)

-- его момент инерции, а -- момент силы трения относительно оси симметрии цилиндра. Подставим в (4) соотношения (5) и выражение для углового ускорения цилиндра , которое следует из (1):

.

В результате, после сокращения на , получим:

. (6)

Если рассматривать качение изолированного цилиндра, то уравнений (3) и (6) достаточно для решения задачи, так как тогда, из-за отсутствия нити, , а два уравнения позволяют определить две неизвестные величины и . В данном случае, сила неизвестна, и приходится рассматривать скольжение бруска и вращение блока.

Рассмотрим скольжение бруска. Запишем второй закон Ньютона в векторном виде

, (7)

а затем, спроектируем его на ось :

. (8)

Здесь, -- сила трения скольжения. Поэтому ее можно рассчитать по формуле . Для нахождения , спроектируем (7) на ось :

.

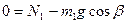Отсюда, и . Подставив данное выражение для силы трения в (8), получим

. (9)

Если бы масса блока равнялась нулю, то сила натяжения была бы одинаковой в пределах всей нити (). Тогда, трех уравнений (3), (6), (9) было бы достаточно для нахождения трех неизвестных . В данном случае, неизвестных четыре (), и приходится использовать еще уравнение динамики вращательного движения блока:

).

Здесь момент силы натяжения 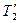ускоряющий и, поэтому, положительный (), момент силы -- тормозящий и, поэтому, отрицательный (), а угловое ускорение блока выражено через с помощью формулы (1).

В результате, сократив на и заменив и на и , получим:

. (10)

Теперь все сводится к решению системы уравнений (3), (6), (9), (10). Сложим эти уравнения почленно:

Приведя подобные члены и проведя сокращение, получим:

1.88 м/с2

Сила трения находится из уравнения (6):

Н.

В заключение напомним, что, если масса блока равна нулю, то сила натяжения одинакова на всем протяжении нити, и, поэтому, нет необходимости использовать уравнение динамики вращательного движения блока.

Кроме того, отметим, что поступательно движущаяся система отсчета, связанная с осью цилиндра, является неинерциальной, так как цилиндр катится с ускорением. Поэтому уравнение динамики вращательного движения цилиндра относительно его оси симметрии должно содержать момент силы инерции. Однако этот момент равен нулю, так как сила инерции приложена в центре масс цилиндра и, следовательно, имеет нулевое плечо.