Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Примеры решения задач.

Задача 1.

Сплошной цилиндр массой m=10 кг и радиусом R=0.5 м, раскрученный до частоты n=5 об/с, кладут в угол комнаты, при этом он вращается на месте. Коэффициент трения между цилиндром и полом . Трением между цилиндром и стеной пренебречь. Определить угловое ускорение цилиндра, число оборотов до его полной остановки и работу сил трения.

Решение

Y

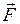
X

На рисунке изображены цилиндр и силы, действующие на него:

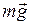- сила тяжести;

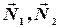- силы реакции со стороны пола и стены соответственно;

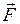- сила трения;

О - ось вращения цилиндра.

Центр масс тела неподвижен; II закон Ньютона в проекции на вертикальную и горизонтальную оси:

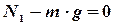
Кроме того,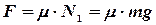

Основной закон динамики вращательного движения твёрдого тела относительно оси вращения О:

,

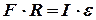где - момент инерции цилиндра, следовательно,

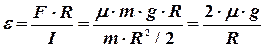
Для определения числа оборотов необходимо определить угол поворота цилиндра вокруг своей оси до его полной остановки. С этой целью используются формулы кинематики:

Знак минус соответствует равнозамедленному движению.

- начальная угловая скорость.

Учитывая, что в момент остановки 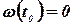, получаем:

и

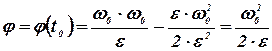
Время, необходимое для остановки

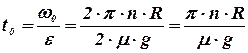
Число оборотов цилиндра

Определим теперь работу силы трения до остановки цилиндра, которая есть произведение силы 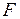на 2π R N-перемещение точки, к которой приложена сила (сила трения направлена против направления перемещения, поэтому ее работа отрицательна):

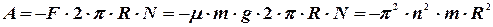
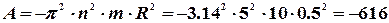Дж

Это же значение работы можно определить из других соображений: работа сил трения равна изменению кинетической энергии тела

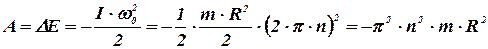
Проведём вычисления:

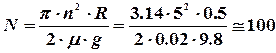оборотов.

Задача 2.

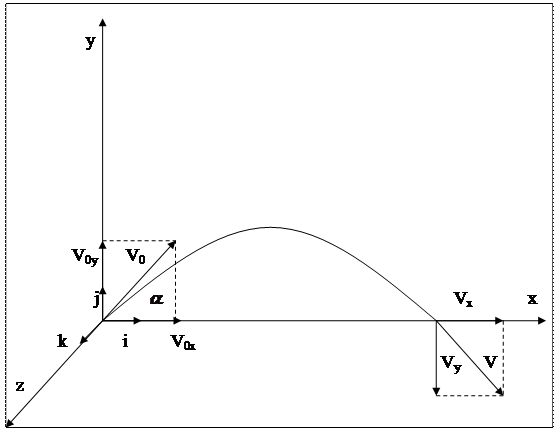
Тело массой 3 кг брошено с начальной скоростью 20 м/с под углом 30⁰ к горизонту. Определить момент импульса тела в конце траектории относительно точки бросания.

Решение.

Момент импульса равен 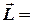[ 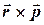], где 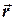-радиус-вектор тела, а 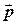- его импульс. В декартовых координатах 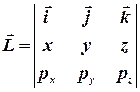, где 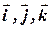- единичные векторы, направленные по осям x, y, z- соответственно. Выберем декартову систему координат так, чтобы ее центр находился в точке бросания, а вектор начальной скорости тела - в плоскости xy, тогда траектория тела будет тоже находиться в плоскости xy.

В момент падения тела координата x равна дальности полёта: 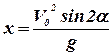, координаты y и z равны нулю: y=0, z=0, проекция скорости тела на ось x равна: V_x=V₀ cosα, проекция скорости тела на ось y равна: V_y=-V₀ sinα, проекция скорости тела на ось z равна: V_z=0.

Тогда

.

Следовательно, момент импульса тела в момент падения направлен против оси z и равен по модулю 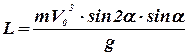= кг м²/c = 2.12 10³ кг м²/c.

Задачу можно решить и не используя формулу для момента импульса материальной точки в декартовых координатах.

Модуль момента импульса материальной точки равен:

L = r mV sinα, где r- модуль радиуса-вектора материальной точки в конце полета, равный дальности полета: 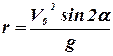, V-модуль скорости тела в конце полета, V = V₀, так как известно, что скорость в конце полета по модулю равна скорости в его начале, α –угол между вектором скорости и радиус-вектором материальной точки в конце полета, он равен углу α между осью х и вектором начальной скорости V₀.

Подставляя, получим что, момент импульса тела L = r mV sinα в момент падения равен: 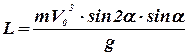= кг м²/c = 2.12 10³ кг м²/c.

Задача 3.

Шар, радиус которого R = 5 см, подвешен на невесомой нити длиной l ₀ = 10 см. Определить относительную погрешность, которую допускают, если, вычисляя период колебаний такого маятника, принимают его за математический маятник длиной l = 15 см.

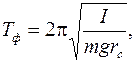Решение. Шар, висящий на нити, представляет собой физический маятник. Его период колебаний T_ф выражается формулой:

(1)

где I– момент инерции маятника относительно оси, проходящей через точку подвеса, m –масса маятника, r_c – расстояние от центра масс до точки подвеса и g –ускорение свободного падения. Если принять маятник за математический, то его период T_м надо находить по формуле:

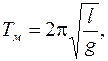(2)

где l –длина маятника. Полагаем согласно условию длину l равной расстоянию от точки подвеса до центра масс шара:

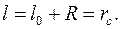(3)

Таким образом, считая маятник математическим, мы заменяем шар материальной точкой, расположенной в его центре, что вызывает некоторую погрешность в вычислении периода.

С помощью формул (1) и (2) найдем отношение периодов T_ф и T_м, учитывая соотношение (3):

(4)

Подставив это значение в (4), получим:

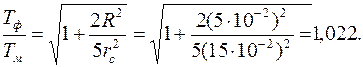Отсюда найдем относительную погрешность в вычислении периода:

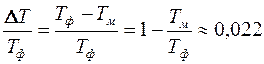или 2, 2%.

Задача 4.

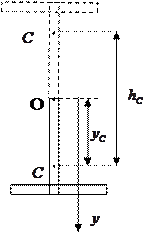Маятник (в виде буквы Т) изготовлен из

двух стержней, имеющих одинаковую массу

и одинаковую длину 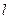. Он может вращаться

без трения вокруг горизонтальной оси,

проходящей через конец одного из стержней

(точка О). Какую минимальную угловую

скорость нужно сообщить маятнику в положении

равновесия, чтобы он совершил полный оборот?

Толщиной стержней пренебречь.