
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Динамика вращательного движения.
|
|
 Момент инерции материальной точки относительно оси вращения Z является мерой инертности для вращательного движения и равен:
Момент инерции материальной точки относительно оси вращения Z является мерой инертности для вращательного движения и равен:
 , где
, где

m - масса материальной точки, r - расстояние от точки до оси Z.
 Момент инерции системы материальных точек относительно оси вращения Z:
Момент инерции системы материальных точек относительно оси вращения Z:
Iz = 

 Момент инерции твёрдого тела относительно оси вращения Z:
Момент инерции твёрдого тела относительно оси вращения Z:

 dV, где
dV, где
V - объём тела, r - расстояние от оси Z до элемента объёма тела dV,
 - плотность тела.
- плотность тела.
 Моменты инерции тел массой m относительно оси, проходящей через центр масс и совпадающей с осью симметрии тела:
Моменты инерции тел массой m относительно оси, проходящей через центр масс и совпадающей с осью симметрии тела:
1) стержня длиной l относительно оси, перпендикулярной стержню 
 ,
,
2) обруча радиуса R (тонкостенного цилиндра)
 ,
,
3) диска (сплошного цилиндра) радиуса R
 ,
,
4) шара радиуса R
 ,
,
 Момент силы
Момент силы 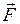 относительно точки О:
относительно точки О:
 ,
,
где  - радиус-вектор, проведённый из точки О к точке приложения силы,
- радиус-вектор, проведённый из точки О к точке приложения силы, 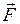 - сила. В скалярной форме:
- сила. В скалярной форме:

 ,
,
где  - плечо силы,
- плечо силы,  - угол между
- угол между 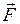 и
и  .
.
 Момент силы относительно оси
Момент силы относительно оси  :
: 
 , где
, где  - составляющая силы, лежащая в плоскости, перпендикулярной оси
- составляющая силы, лежащая в плоскости, перпендикулярной оси  ,
,
 Теорема Штейнера:
Теорема Штейнера:  , где
, где 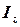 - момент инерции тела относительно произвольной оси
- момент инерции тела относительно произвольной оси  ,
,  - момент инерции этого же тела относительно оси, проходящей параллельной первой через его центр масс, а
- момент инерции этого же тела относительно оси, проходящей параллельной первой через его центр масс, а  - расстояние между осями.
- расстояние между осями.
 Кинетическая энергия тела, вращающегося вокруг неподвижной оси
Кинетическая энергия тела, вращающегося вокруг неподвижной оси  :
:  , где
, где  - момент инерции тела относительно оси
- момент инерции тела относительно оси  , а
, а  z - его угловая скорость.
z - его угловая скорость.
 Кинетическая энергия катящегося тела:
Кинетическая энергия катящегося тела: 
 , где
, где 


 - скорость центра масс тела, а Ic - момент инерции тела относительно оси, проходящей через центр масс.
- скорость центра масс тела, а Ic - момент инерции тела относительно оси, проходящей через центр масс.
 Потенциальная энергия тела:
Потенциальная энергия тела:  , где hc - высота центра масс тела относительно нулевого уровня.
, где hc - высота центра масс тела относительно нулевого уровня.
 Координата центра масс составного тела:
Координата центра масс составного тела:  ,
,
где  и
и  соответственно масса и координата центра масс i тела.
соответственно масса и координата центра масс i тела.
 Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси z:
Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси z:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 z,
z,
где  - проекция на ось z результирующего момента внешних сил, действующих на тело,
- проекция на ось z результирующего момента внешних сил, действующих на тело,
 z- угловое ускорение,
z- угловое ускорение,  - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.
 Работа при повороте тела на угол
Работа при повороте тела на угол  z относительно оси
z относительно оси  :
:
 z, где
z, где
 - проекция момента приложенной силы на ось
- проекция момента приложенной силы на ось  .
.
 Момент импульса
Момент импульса  материальной точки относительно точки О:
материальной точки относительно точки О:
 ,
,
где  - радиус-вектор, проведённый из точки О к материальной точке,
- радиус-вектор, проведённый из точки О к материальной точке, 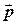 - импульс. В скалярной форме:
- импульс. В скалярной форме:

L =l p,
Где:  - плечо импульса,
- плечо импульса,  - угол между
- угол между 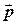 и
и  .
.
 Момент импульса твердого тела относительно оси вращения z:
Момент импульса твердого тела относительно оси вращения z:
Lz=Iz ω Z
|
|
