Основні поняття та закони хімії

Молекула - це найменша частинка індивідуальної речовини, яка зберігає її хімічні властивості й склад та здатна до самостійного існування.

Якщо молекули складаються з однакових атомів, то речовину називають простою (наприклад, Н₂, О₂, О₃, S₄, S₈, Не, P₄ тощо). Проста речовина - це форма існування хімічного елемента у вільному стані. У природі певний хімічний елемент може утворювати різні прості речовини. Це явище називають алотропією, а різні форми простої речовини, які відповідають одному хімічному елементу, називають алотропними формами (модифікаціями).

Якщо молекула речовини складається з різних атомів, то речовину називають складною (або хімічною сполукою), наприклад, СО₂, Н₂SО₄, KОН, NH₄Cl тощо.

Кожна хімічна сполука характеризується певним складом (природою та кількістю різних атомів у її молекулі), будовою (просторовим розміщенням атомів у молекулі), а також певними фізичними та хімічними властивостями.

Розміри атомів і молекул надзвичайно малі, тому мізерні й їх маси (наприклад, m (H) = 7, 305 × 10^-26 к г; m (CO₂) = 1, 66 × 10^-27 к г). У зв’язку з цим вираження мас атомів і молекул в одиницях СІ дуже незручне. За пропозицією Д. Дальтона для вираження мас атомів і молекул у хімії застосовують відносні величини.

Зокрема з 1961 р. для цього використовують карбонову (вуглецеву) шкалу. За одиницю у вуглецевій шкалі відносних атомних мас елементів умовно прийнято 1/12 маси атома ізотопу Карбону :

1 а.о.м. = ;

1 а.о.м. = = 1, 66 · 10^-27 к г.

Відносна атомна маса А_r (Х) - це відношення маси атома елемента до 1/12 частини маси атома ізотопу Карбону з масовим числом дванадцять, . Відносну атомну масу наведено в періодичній таблиці Д. І. Менделєєва, вона - безрозмірна величина. Майже в усіх елементів відносні атомні маси - дробові. Це пояснюється тим, що хімічні елементи в природі знаходяться у вигляді різних ізотопів. Наведена у таблиці Д. І. Менделєєва відносна атомна маса є середньостатистичною між атомними масами ізотопів з урахуванням вмісту ізотопів у природі.

Відносною молекулярною масою речовини М_r (Х) називають відношення маси молекули речовини до 1/12 маси атома ізотопу Карбону з масовим числом дванадцять . Це також безрозмірна величина.

Відносну молекулярну масу можна розрахувати як суму відносних атомних мас елементів, що входять до складу молекули, наприклад:

М_r (H₂SO₄) = 2 А_r (H) + А_r (S) + 4 А_r (O);

М_r (H₂SO₄) = 2 × 1, 01 + 32, 06 + 4 × 16, 00 = 98, 08;

М_r (NaOH) = А_r (Na) + А_r (O) + А_r (H);

М_r (NaOH) = 22, 99 + 16, 00 + 1, 01 = 40, 00.

Кількість речовини n (x) характеризує розмір порції речовини чисельністю певних частинок (формульних одиниць), які містяться в цій порції. Формульною одиницею може бути атом, молекула, іон, радикал тощо. Одиницею вимірювання кількості речовини є моль.

Моль - це порція речовини, що містить 6, 022 × 10²³ (число Авогадро) формульних одиниць. У СІ також застосовують одиницю вимірювання 1 кіломоль, який містить кількість частинок, що перевищує число Авогадро в 1000 разів, тобто дорівнює 6, 022 × 10²⁶ формульних одиниць.

Число Авогадро визначається кількістю атомів у 0, 012 к г ізотопу Карбону з масовим числом дванадцять (N _A = 6, 022 × 10²³ моль^-1).

Молярна маса М (Х) - це відношення маси порції речовини до кількості речовини в цій порції:

М (Х) = m (Х)/ n (Х), (2.1)

тобто молярна маса - це маса 1 моль речовини виражена у грамах.

Молярна маса речовини чисельно дорівнює відносній молекулярній масі цієї речовини, її, як правило, виражають у г/моль. Наприклад, М (H₂SO₄) = 98, 08 г /моль; М (NaOH) = 40, 00 г /моль. У СІ молярна маса вимірюється в кг/моль: М (СО₂) = 44 г /моль = 4, 4 × 10^-2 к г /моль.

До стехіометричних законів належать закони збереження маси, сталості складу, Авогадро, кратних відношень, а також закон еквівалентів.

Закон збереження маси речовини є одним з основних законів хімії. Уперше його сформулював 1748 року М. В. Ломоносов (експериментально він довів його 1756 року). Вже пізніше (у 1783 р.) цей закон підтвердив французький хімік Лавуазьє.

У сучасному вигляді закон збереження маси речовини формулюється таким чином: маса речовин, які вступають у хімічну реакцію, дорівнює масі речовин, які утворюються внаслідок цієї реакції.

Цей закон справедливий тільки для тих хімічних реакцій, які перебігають без виділення або поглинання такої великої кількості енергії, що це може приводити до експериментально встановленого переходу матерії з форми речовини у форму поля (наприклад, ядерні перетворення тощо). Отже, у класичному формулюванні закон збереження маси речовини має не абсолютне, а відносне значення.

Закон збереження маси речовини в його хімічному розумінні можна тлумачити і таким чином: кількість атомів кожного елемента до хімічної реакції дорівнює кількості його атомів після реакції. Саме у такому вигляді цей закон використовують для складання рівнянь хімічних реакцій.

Речовини характеризують певним якісним, кількісним або атомним складом.

Якісний склад показує, які елементи утворюють дану речовину. Наприклад, для гідроген пероксиду Н₂О₂ – це Гідроген і Оксиген.

Кількісний (ваговий) склад – це співвідношення мас усіх елементів, що утворюють дану речовину. Зокрема, кількісний склад для пероксиду гідрогену описують співвідношенням:

m (H): m (O) = 1: 16.

Знаючи формулу хімічної сполуки та відносні атомні маси елементів, що її утворюють, можна розрахувати кількісний склад даної сполуки. Наприклад, для хімічної сполуки А_аВ_b:

m (A): m (B) = (a × А_r (A)): (b × А_r (B)). (2.2)

Можна розв’язати і зворотну задачу, тобто знайти відношення a: b, виходячи з кількісного складу речовини і відносних атомних мас елементів:

(2.3)

Відношення a: b характеризує елементний склад речовини. Знаючи атомний склад речовини, можна записати найпростішу (емпіричну) формулу хімічної сполуки, наприклад, для гідроген пероксиду Н _a О _b атомний склад a: b = 1: 1 дає найпростішу формулу НО, яка відрізняється від реальної, тому що молярна маса гідроген пероксиду дорівнює 34 г /моль.

Отже, для виведення істинної формули речовин, що мають молекулярний склад (тобто складаються з окремих молекул), треба знати окрім атомного складу їх молярну масу М (Х). Оскільки М (Н _a О _b)= 34 г /моль, індекси при символах елементів у формулі гідроген пероксиду у мають бути подвоєними, а його хімічна формула становитиме Н₂О₂.

Розрахунки кількостей реагентів, необхідних для проведення перетворення або отриманих внаслідок реакції, зазвичай, виконують за рівняннями хімічних реакцій. Якщо вихідні речовини А і В внаслідок хімічної реакції утворюють продукт D за рівнянням реакції

аА + bВ = dD,

маси реагуючих та отриманих речовин знаходяться у такому співвідношенні:

m (A): m (B): m (D) = (a × М_r (A)): (b × М_r (B)): (d × М_r (D)). (2.4)

Закон кратних відношень було сформульовано Д. Дальтоном 1808 року. Його формулюють таким чином: якщо два елементи, сполучаючись між собою, утворюють дві або кілька речовин, то на вагову одиницю одного з них припадають такі вагові кількості другого, що вони відносяться між собою як прості кратні числа.

Закон сталості складу був визначений Ж. Прустом у 1801 р. Згідно із цим законом кожна індивідуальна хімічна сполука має певний та сталий елементний склад незалежно від способу її одержання та місцезнаходження у природі.

Однак за нашого часу цей закон уже не є загальним, оскільки крім сполук, які мають сталий склад - дальтонідів, існують також сполуки змінного складу - бертоліди (деякі оксиди металів, бориди, карбіди, нітриди, сульфіди металів тощо). Отже, цей закон має певні межі застосування.

Згідно з законом Авогадро (1811 р.), у рівних об’ємах різних газів, узятих за однакових умов (температури і тиску), міститься однакова кількість молекул.

Відомо два наслідки із цього закону:

1. Маси рівних об’ємів різних газів за однакових температури і тиску відносяться між собою як їх молярні маси:

, якщо V (X ₁) = V (X ₂). (2.5)

2. Один моль будь-якого газу за однакових умов займає однаковий об’єм, що має назву молярного (V_М).

За нормальних умов (н. у.): T = 273, 15 К (відповідає 0 °С), р = 101 325 Па (1 атм; 760 мм. рт. ст.), молярний об’єм V ⁰ _М = 22, 414 л/моль або 22, 414 × 10^-3 м³/моль.

Молярний об’єм – це відношення об’єму газу до кількості речовини в цьому об’ємі:

V_M = . (2.6)

Відносна густина одного газу за іншим – це відношення мас рівних об’ємів двох різних газів за однакових температури і тиску:

, якщо V (X ₁) = V (X ₂),

або . (2.7)

Найчастіше відносну густину визначають за воднем або за повітрям (усереднена молярна маса повітря М _ПОВ = 29 г /моль):

, звідки М (Х ₁) =

D _ПОВ = , тоді М (Х ₁) = D _ПОВ × 29 г /моль.

Для кількісних розрахунків реагентів, що знаходяться в газоподібному стані, використовують об’єднаний закон газового стану, вираженням якого є рівняння стану ідеального газу:

, (2.8)

де V ₀ – молярний об’єм газу за нормальних умов (р ₀, Т ₀); n – загальна кількість молів усіх газів.

Підстановка значень р ₀, V ₀ і Т ₀ дозволяє розрахувати універсальну газову сталу (). Тоді рівняння Менделєєва - Клапейрона має вигляд

(3.1)

причому чисельні значення R залежать від одиниць вимірювання тиску й об’єму газу: R = 8, 314 Дж/(моль · К) або R = 0, 082 атм · л/(моль · К).

Хімічним еквівалентом елемента (Е) називають умовну частку атома хімічного елемента (1 /z *), якій у хімічній реакції відповідає атом Гідрогену або хімічний еквівалент іншого елемента.

Наприклад, хімічний еквівалент Йоду в молекулі HІ складає один його атом (z *(І) = 1, де z * - число еквівалентності Йоду, яке чисельно дорівнює валентності елемента у сполуці). Хімічний еквівалент Селену в молекулі H₂Sе складає 1/2 атома Селену, оскільки на один атом Гідрогену припадає 1/2 атома Селену (z *(Sе) = 2, Е = 1 /z * = 1/2).

Якщо елемент утворює декілька хімічних сполук, виявляючи в них різні валентності, його хімічні еквіваленти в цих сполуках будуть різними. Наприклад, у сполуці MnO₂ хімічний еквівалент Мангану складає 1/4 атома Мангану (z *(Mn) = 4, Е = 1 /z * = 1/4), а у сполуці KМnO₄ - 1/7 атома Мангану (z *(Mn) = 7, Е = 1 /z * = 1/7).

Хімічні еквіваленти можна визначити безпосередньо з даних хімічного аналізу сполуки або на основі кількісного дослідження реакції заміщення у хімічній сполуці одного елемента іншим.

Молярну масу хімічних еквівалентів елемента можна розрахувати за формулою

М (2.10)

Наприклад: М () = М () = 35, 5 г /моль; М () = М ()= 8 г /моль; М () = М () = 1 г /моль; М () = 16 г /моль.

Молярну масу еквівалентів сполуки можна розрахувати, додаючи молярні маси еквівалентів усіх елементів, що складають цю сполуку.

Згідно із законом еквівалентів (Ріхтер, 1800 р.; Дальтон, 1803 р.), маси реагуючих між собою речовин відносяться одна до одної як молярні маси хімічних еквівалентів цих речовин:

(3.2)

Тобто речовини реагують між собою еквівалентними кількостями:

n ( X ₁) = n ( X ₂), де n ( X_i) = (2.12)

Закон еквівалентів зручно використовувати для знаходження хімічних формул сполук, а також для кількісних розрахунків без використання рівнянь хімічних реакцій.

Молярний об’єм хімічних еквівалентів простої газоподібної речовини - це об’єм, який займає молярна маса еквівалентів цієї речовини за нормальних умов.

Наприклад: V ( Н) = = 22, 4/2 = 11, 2 (л/моль);

V () = = 22, 4/4 = 5, 6 (л/моль);

V ( Cl) = = 22, 4/2 = 11, 2 (л/моль).

3.2. Запитання для самостійної підготовки

1. Дайте означення матерії. Які форми існування матерії відомі? Чим відрізняється речовина від поля?

2. Що таке хімічний елемент? Які речовини називають простими, а які - складними? Що таке явище алотропії, чим воно обумовлене? Наведіть приклади.

3. Що таке атомна одиниця маси, відносні атомна і молекулярна маси?

4. Чим відрізняються молекулярна і молярна маси речовини? Що таке моль?

5. Дайте означення поняттям: хімічний еквівалент, число еквівалентності, молярна маса хімічних еквівалентів елемента.

6. Чи завжди еквівалент елемента однакова величина? Наведіть приклади елементів, еквіваленти яких можуть змінюватись.

7. Сформулюйте закони збереження маси речовин, закон Авогадро та наслідки з нього. Що таке відносна густина одного газу за іншим?

8. Сформулюйте закон еквівалентів. Як можна розрахувати атомну масу елемента за допомогою закону еквівалентів? Які дані для цього потрібні?

9. Які оксиди є солетворними та несолетворними?

10. Які оксиди належать до основних, кислотних і амфотерних? Які їх хімічні властивості?

11. Які гідроксиди належать до основ, кислот? Як їх можна одержати, які хімічні властивості вони виявляють?

12. Які хімічні властивості амфотерних гідроксидів? Як їх можна одержати?

13. Що називають реакцією нейтралізації?

14. Що таке солі? У чому полягають особливості одержання середніх, кислих і основних солей? Які їх хімічні властивості?

4. Приклади розв’язання типових задач з теми 3

Задача 1. Визначити: а) кількість молів атомів у 150 г кремнію; б) кількість атомів у 50 г кремнію; в) кількість молів молекул води Н₂O у 50 грамах; г) масу однієї молекули СO₂ у грамах.

Розв’язання. а) Оскільки М (Si) = 28, 09 г /моль, тоді кількість молів атомів силіцію:

n (Si) = 5, 34 (моль атомів);

б) кількість атомів Силіцію N_X (Si), що містяться у 50 г речовини:

N_X (Si) = (атомів);

в) кількість молів води у 50 грамах:

n (Н₂O) = 2, 78 (моль);

г) для визначення маси молекули (атома) у грамах використовуємо формули:

(3.3) (2.13)

m ₀(СO₂) = (г).

Задача 2. Визначити масу одного літра хлору (н. у.).

Розв’язання. За формулою:

n (Cl₂) = ,

де V _M – молярний об’єм газу, розраховуємо масу одного літра хлору (н.у.), враховуючи, що маса одного літра за визначенням – густина d, г /л. Тоді

M (Cl₂) = ;

M (Cl₂) = 71, 0 г /моль.

Отже,

r(Сl₂) =

Тобто маса 1 літра хлору за н. у. дорівнює 3, 17 г.

Задача 3. Обчислити об’єм, який займають: а) 64 г кисню; б) 2, 7× 10²² молекул кисню (н. у.).

Розв’язання.

а) розраховуємо кількість речовини кисню:

n (O₂) =

тодіоб’єм кисню становить:

V (O₂) = n (O₂) V ⁰_М = 2 × 22, 4 = 44, 8 (л).

б) кількість речовини кисню становить:

n (O₂) =

тоді об’єм кисню

V (O₂) = n (O₂) V ⁰_M = 0, 045 × 22, 4 = 1 (л).

Задача 4. У закритій посудині знаходиться газ при температурі 25 °С. До якої температури треба нагріти цей газ, щоб збільшити його тиск у 2, 5 рази?

Розв’язання. Рівняння Менделєєва - Клапейрона має вигляд (3.1) або:

pV = 1 000 nRT = , (2.14)

де m – маса газу, г; М (Х) – молярна маса газу, г /моль; R – універсальна газова стала (8, 31 Дж/(моль× К)); Т – температура, К; р – тиск, Па; V – об’єм, л.

За умовою (див. об’єднаний закон газового стану):

,

де р ₁ = 2, 5 р; V ₁ = V; T = 273 + 25 = 298 К.

Тоді

Отже, T ₁ = 2, 5 T = 2, 5 × 298 = 745 К = 472 °C.

Задача 5. Знайти: а) відносну густину амоніаку за повітрям; б) молярну масу невідомого газу, якщо відносна густина його за воднем дорівнює 15.

Розв’язання: а) відносна густина амоніаку за повітрям:

D _пов(NH₃) =

б) молярна маса невідомого газу:

M (Х) = (Х) M (H₂) = 15 × 2 = 30 г /моль.

Задача 6. Визначити вміст елементів у відсотках (масові частки) в оксиді Mn₂O₇ . Розв’язання. Масова частка w(х) або вміст елемента у відсотках – це маса елемента, що міститься в 100 г хімічної сполуки.

Знаючи, що M (Mn) = 54, 94 г /моль і М (Mn₂O₇) = 221, 88 г /моль, складаємо пропорцію:

221, 88 г сполуки містить 2 × 54, 94 г Mn;

100 г сполуки містить х г Mn.

Тоді масові частки Мангану та Оксигену у сполуці Мn₂O₇ становитимуть:

w(X) = m (X)/ m (Мn₂O₇),

w(Mn) =

w(О) = 100 – 49, 52 = 50, 48 %.

Задача 7. Мінерал містить 75 % сполуки FeS. Визначити, яка маса цього мінералу містить 1 к г Феруму.

Розв’язання. Обчислюємо масу сульфіду феруму FeS, у якій міститься 1 к г Феруму, якщо M (FeS) = 87, 91 г /моль, M (Fe) = 55, 85 г /моль. Для цього складаємо пропорцію:

87, 91 г FeS містить 1 × 55, 85 г Fe;

х FeS містить 1000 г Fe.

Тоді маса сульфіду феруму

х =

Розрахуємо масу мінералу, в якому міститься 1к г феруму:

m _{мінералу} = 1 574, 04 / 0, 75 = 2 098, 72 г = 2, 099 (к г).

Задача 8. Обчислити: а) молярну масу хімічних еквівалентів Мангану в оксиді MnO₂; б) молярні маси еквівалентів сполук: PbO; Cu(OH)₂; HNO₂; AlCl₃.

Розв’язання. а) Валентність Мангану в оксиді MnO₂ дорівнює чотирьом, тобто число еквівалентності z *(Mn) = 4. Тоді молярнa масa хімічних еквівалентів Мангану становитиме:

б) Молярна маса еквівалентів оксиду PbO:

де i (Pb) – індекс при атомі Плюмбуму; у даному випадку i (Pb) = 1.

Молярна маса еквівалентів основи Cu(OH)₂:

де j – кількість гідроксильних груп у формулі основи; j = 2.

Молярна маса еквівалентів кислоти HNO₂ :

де і – кількість атомів Гідрогену в формулі кислоти; і = 1.

Молярна маса еквівалентів солі AlCl₃:

де i (Al) – індекс при атомі Алюмінію; у даному випадку і (Al) = 1.

Задача 9. За нормальних умов маса 0, 5 л газу становить 1, 806 г. Обчислити: а) кількість речовини; б) відносну молекулярну масу газу; в) кількість молекул у

цьому об’ємі.

Розв’язання. а) Розраховуємо кількість речовини, що займає об’єм 0, 5 л:

n (X) =

б) Оскільки n (X) = , молярна маса невідомого газу становить:

М (X) =

Відносна молекулярна маса газу чисельно дорівнює молярній масі, тому

M_r (X) = 81.

в) Розраховуємо кількість молекул у цьому об’ємі газу

N_X = n (X) N _A = 0, 0223 × 6, 02 × 10²³ =1, 34 × 10²² (молекул).

Задача 10. Обчислити молярну масу еквівалентів металу, якщо його хлорид містить 65, 57 % Хлору. Визначити, який це метал, якщо відомо, що в хлориді він тривалентний.

Розв’язання. Згідно з законом еквівалентів (3.2):

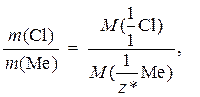
але оскільки w(X) = m (X)/ m (сполуки), то

закон еквівалентів можна записати таким чином:

ω (Me) = 100 – ω (Cl‌) = 100 – 65, 57 = 34, 43 %.

Розраховуємо молярну масу еквівалентів металу:

Щоб визначити, який це метал, потрібно розрахувати його молярну масу:

М (Ме) = = 18, 62 × 3 = 55, 85 (г /моль).

За допомогою періодичної таблиці знаходимо, що цей метал – Ферум (Fe).

Задача 11. Одна й та сама маса металу потрібна для взаємодії і з 1, 78 г сірки, і з 8, 89 г брому. Визначити молярну масу хімічних еквівалентів Брому, якщо молярна маса хімічних еквівалентів Сульфуру становить 16 г /моль.

Розв’язання. Згідно із законом еквівалентів (3.2) запишемо:

Отже, отримуємо:

Тоді

(г/моль).

Задача 12. На відновлення з 8, 0 г оксиду двовалентного металу витрачається 2, 24 л водню (н.у.). Обчислити молярну масу еквівалентів металу. Чому дорівнює відносна атомна маса металу? Який це метал?

Розв’язання. Якщо одна з речовин знаходиться в газоподібному стані, закон еквівалентів можна записати у вигляді:

(2.16)

де

V 11, 2 л/моль.

Розраховуємо молярну масу еквівалентів оксиду металу МеО:

Оскільки

М = М + М ;

М = М = 8, 00 г /моль,

то

М = М - М = 40, 0 – 8, 00 = 32, 0 (г /моль).

Якщо метал двовалентний, відносна атомна маса металу дорівнює

A_r (Me) = 32, 0 × 2 = 64, 0. Отже, невідомий метал – Купрум.

Задача 13. Яка маса металу взаємодіє з 500 см³ кисню (н. у.), якщо молярна маса хімічних еквівалентів металу дорівнює 12, 16 г /моль.

Розв’язання. Згідно із законом еквівалентів (3.2):

де

= 5, 6 (л/моль).

Отже,

5. Будова атома. Періодичний закон

і періодична система Д. І. Менделєєва

Програмні питання

Діалектика розвитку уявлень про будову атома. Ядерна модель атома Резерфорда. Будова атома Гідрогену за теорією Бора.

Поняття про двоїсту корпускулярно-хвильову природу електрона. Квантово-механічна модель атома. Принцип невизначеності Гейзенберга. Атомні орбіталі, типи атомних орбіталей. Рівняння Шредінгера. Квантові числа (головне, орбітальне, магнітне та спінове). Розміщення електронів на атомних орбіталях: принцип найменшої енергії, правила Клечковського, принцип заборони Паулі, правило Хунда. Електронні формули атомів хімічних елементів. Електронні родини елементів.

Періодичний закон Д. І. Менделєєва. Структура періодичної системи та різновиди періодичних таблиць елементів. Періодичність зміни властивостей хімічних елементів; характеристика властивостей елементів за їх положенням у періодичній системі; s -, р -, d - і f -елементи.

Енергія іонізації та енергія спорідненості до електрона як кількісні характеристики відповідно металічних і неметалічних властивостей. Електронегативність елементів.

5.1. Будова атома

Ця тема є однією з базових у курсі та потрібна для вивчення практично всіх подальших розділів програми. Результатом її засвоєння має бути вміння характеризувати квантовий стан електронів, складати електронні конфігурації атомів елементів, визначати за ними положення елемента в періодичній системі, передбачати його хімічні властивості.

Як зазначалося раніше, атом – це найменша електрично нейтральна елементарна частинка, яка зберігає хімічні властивості елемента. Атом містить позитивно заряджене ядро, у якому зосереджено практично всю його масу, та

електрони, що обертаються навколо ядра.

Ядро, у свою чергу, складається з нуклонів: позитивно заряджених протонів та електрично нейтральних нейтронів. Ядро - фундаментальна основа атома, яка характеризує індивідуальність хімічного елемента. Заряд ядра атома z, виражений в умовних одиницях, визначається кількістю протонів у ядрі та збігається з порядковим номером елемента в періодичній системі.

Електрони – негативно заряджені елементарні частинки; вони зумовлюють розміри атома та його хімічні властивості. Кількість електронів у атомі дорівнює кількості протонів у ядрі. Деякі характеристики нуклонів і електронів наведені в табл. 5.1.

Таблиця 5.1.

Основні характеристики елементарних частинок

Елементарна частинка	Сим- вол	Маса покою	Заряд	Спін
m, кг	а.о.м.	Кл	Умовний
Протон	p	1, 673× 10-27	1, 007276	1, 602× 10-19	+1
Нейтрон	n	1, 675× 10-27	1, 008665
Електрон	e	9, 110× 10-31	0, 000549	-1, 602× 10-19	-1

Хімічні властивості атомів зумовлені електронною конфігурацією і, насам-перед, кількістю та розташуванням електронів на валентних рівнях атома, оскільки саме вони беруть участь в утворенні хімічних зв’язків.

Сучасні теорії будови атома ґрунтуються на законах квантової (хвильової) механіки, яка базується на уявленні про квантування енергії, гіпотезі про двоїсту природу мікрочастинок, зокрема електрона, та хвильовому характері його руху навколо ядра. Згідно з постулатом М. Планка (1900 р.), енергія випромінюється дискретно тими атомами, які перебувають у стані коливання, причому кожен з них випромінює енергію певної частоти. М. Планк назвав найменшу порцію енергії, яку можна виділити в одному акті випромінювання квантом, або фотоном. Енергія кванта визначається за рівнянням Планка:

Е = h n,

де Е – величина енергії кванта; h – стала Планка (h = 6, 62517× 10^-34 Дж× с); n - частота коливань. Поглинаючи квант енергії, атом переходить із стаціонарного стану з мінімально можливим для нього запасом енергії в збуджений стан.

Згідно з гіпотезою Луї де Бройля, двоїсту природу має кожний матеріальний об’єкт, тобто з кожною частинкою, яка рухається, зв’язана його особиста хвиля, довжина якої l залежить від маси частинки m та швидкості її руху v:

Однак тільки для мікрочастинок (електронів, нейтронів, протонів та ін.), маси яких дуже малі, довжини їх дебройлівських хвиль сягають вимірних значень.

Згідно з принципом невизначеності В. Гейзенберга (1925 р.), неможливо одночасно точно визначити положення та імпульс будь-якої мікрочастинки, оскільки невизначеність положення D х і невизначеність імпульсу D(mv_x) зв’язані співвідношенням:

D х D(mv_x) або D х D v_x .

Тому, за принципом Гейзенберга, рух електрона (а також будь-якої елементарної частинки) неможливо охарактеризувати певною траєкторією.

Математично поведінку мікрочастинок описують за допомогою рівняння Шредінгера. Правомірність емпіричного вибору рівняння стоячої хвилі як моделі була доведена тим, що розв’язок рівняння Шредінгера дає значення енергій електронів, які добре збігаються з експериментальними даними атомних спектрів.

Після підстановки хвильової функції y(x, y, z) (псі-функції) в рівняння стоячої хвилі, а також використання співвідношення Луї де Бройля, Е. Шредінгер одержав таке диференціальне рівняння:

,

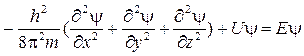де y - хвильова функція (псі-функції), яка характеризує рух електрона при заданій його повній енергії E та залежить від координат тривимірного простору x, y, z; m – маса електрона; U – потенціальна енергія електрона.

Точне розв’язання рівняння Шредінгера можливе тільки для одно-електронного атома, наприклад для атома Гідрогену. Для багатоелектронних атомів це рівняння має безліч розв’язків. Тому для одержання достовірних значень енергії електрона слід вводити граничні умови, а саме: хвильова функція має бути скінченною, безперервною та однозначною.

Розв’язок рівняння Шредінгера - хвильову функцію y - називають атомною орбіталлю (АО). Вона характеризує форму й об’єм частини простору, у якому ймовірність знаходження електрона становить більше 95 %.

Певний фізичний зміст має квадрат хвильової функції за абсолютною величиною ½ y(x, y, z)½ ², який визначає ймовірність знаходження електрона в точці простору з координатами x, y, z. Тому відомості про поведінку електрона в атомі та його рух навколо ядра мають імовірнісний характер.

Квантово-механічна модель, а саме область найімовірнішого розташування електрона у просторі атомного ядра з координатами х, y, z, має назву електронної хмари.

З рівняння Шредінгера безпосередньо випливає потреба введення ще трьох безрозмірних цілочислових параметрів – так званих квантових чисел, які відповідають трьом ступеням свободи руху електрона в атомі.

Головне квантове число (n = 1, 2, 3, …, ) приблизно характеризує енергію рівня та розміри електронної хмари.

Орбітальне (побічне) квантове число (l = 0, 1, 2, …, n - 1) уточнює енергію підрівня і визначає форму атомної орбіталі. Так s -атомні орбіталі мають форму кулі, р -АО - форму гантелі, d -АО мають чотирьохпелюсткову конфігурацію, а f -АО мають складну восьмипелюсткову конфігурацію.

Для характеристики форми АО користуються спеціальними символами, що пов’язані з характером спектральних ліній:

символ орбіталі s p d f …

чисельне значення l 0 1 2 3 …

Магнітне квантове число (m_l = - l …0…+ l) характеризує розміщення атомних орбіталей у просторі. Воно може набувати цілочислових додатних та від’ємних значень від мінус l до + l включно з нулем, тобто кількість можливих значень m_l дорівнює 2 l + 1.

Атомну орбіталь (y ) можна однозначно охарактеризувати, якщо для неї відомі значення трьох квантових чисел: n, l, m_l. Атомні орбіталі з приблизно однаковим запасом енергії однаковим значенням n утворюють енергетичний рівень.

Енергетичним підрівнем називають сукупність АО, які мають однакову енергію і форму. Орбіталі з однаковою енергією називаються виродженими. Оскільки енергію атомної орбіталі визначають головне й орбітальне квантові числа, то атомні орбіталі одного енергетичного підрівня мають, відповідно, однакові значення n і l.

Стан електрона в атомі описують за допомогою чотирьох квантових чисел, оскільки електрон має власний магнітний момент, що не пов’язаний з його орбітальним рухом навколо ядра, який називають спіном.

Спін електрона (або спінове квантове число m_S) – така сама фундаментальна властивість електрона, як маса і заряд. Він може набувати двох значень: 1/2 або -1/2. Схематично спінове квантове число позначають стрілочками: ­ (m_S = 1/2); ¯ (m_S = -1/2). Спін електрона визначає напрямок вектора його власного магнітного моменту відносно зовнішнього магнітного поля.

Заповнення електронами рівнів та підрівнів відбувається згідно з принципом найменшої енергії (принципом В.Паулі, правилом Ф.Гунда, правилами В.М.Клечковського).

По принципу найменшої енергії, електрони заповнюють атомні орбіталі у порядку зростання їх енергії.

Згідно з принципом Паулі, в атомі не може бути двох електронів з однаковим набором усіх чотирьох квантових чисел.

Формулювання двох правил Клечковського має вигляд:

1) зі зростанням заряду ядра атома електрони заповнюють атомні орбіталі в порядку зростання суми головного і орбітального квантових чисел n + l;

2) у разі однакових значень суми n + l першою заповнюється електронами атомна орбіталь, яка має менше значення головного квантового числа n.