Розділ 3. Електромагнітна індукція

6.1. Явище електромагнітної індукції. Досліди Фарадея

В основі електродинаміки змінних полів лежить фундаментальний закон електромагнітної індукції, відкритий дослідно у 1831 р. видатним англійським вченим М. Фарадеєм. Спрощено суть цього закону по­лягає у виникненні струму в довільному замкненому провідному контурі при зміні магнітного потоку, що пронизує цей контур.

X. Ерстед у 1820 р. відкрив, що навколо провідників зі струмом вини­кає магнітне поле. Пізніше, у цьому ж році, А. Ампер встановив, що на провідники зі струмом у магнітному полі діє пондеромоторна сила. Ре­зультати цих досліджень стали основою припущення, що й електричне поле можна одержати за рахунок магнітного.

Рис. 6.1 Рис.6.2

Для перевірки цієї гіпотези були прове­дені різноманітні експерименти. Один із них полягав у спробі виявити струм у замкненому провіднику, розміщеному біля іншого провідника, по якому проходив постійний електричний струм. Ці дослідження при всій старанності їх проведення дали негативний результат. Лише М. Фарадей у 1831 р. звернув увагу на те, що електричні ефекти ви­никають тільки під час зміни магнітного поля. Якщо в одному про­віднику змінювати електричний струм, то в сусідньому також вини­кає струм. Аналогічний результат одержують тоді, коли біля замкне­ного провідника переміщають магніт. Електричний струм в обох ви­падках наводиться (індукується) змінним магнітним полем. Такий струм називають індукційним, а явище виникнення струму в замкне­ному провіднику під дією змінного магнітного поля — явищем елек­тромагнітної індукції.

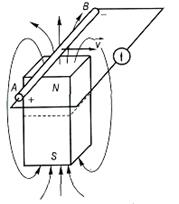
Розглянемо кілька дослідів, які зумовили відкриття явища елек­тромагнітної індукції і дали можливість всебічно вивчити його особ­ливості. Розмістимо провідник АВ завдовжки l у полі постійного маг­ніту і до його кінців А і В приєднаємо чутливий гальванометр (рис. 6.1). Якщо провідник і магніт перебувають у відносному спо­кої, то стрілка гальванометра не відхилятиметься, вказуючи, що струму в замкненому провідному контурі немає. Як тільки провідник АВ у полі постійного магніту починають переміщати, то в колі з'яв­ляється індукційний струм і стрілка гальванометра відхилятиметься. При цьому напрям відхилення стрілки гальванометра, а отже, і на­прям струму залежать від напряму переміщення провідника АВ у маг­нітному полі. Яка причина виникнення індукційного струму? У про­віднику АВ є позитивні іони кристалічної ґратки і вільні електрони. Під час руху провідника в магнітному полі зі швидкістю 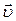разом з ним переміщаються і заряди. На ці заряди вздовж провідника l діє сила Лоренца 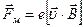. Позитивні заряди зв'язані з кристалічною граткою і переміщатися не мо­жуть, а вільні електрони, при вка­заному на рис. 7.1 напрямі швидкості, будуть зміщатися до кінця провідника В і заряджатимуть його негативно. При цьому кінець провідника А збіднюється елек­тронами і заряджається позитивно. Сила Лоренца 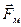в цьому досліді відіграє роль сторонньої сили. Всередині провідника АВ виникає електричне поле, напруженість якого обчислюють з умови рів­ності сил, що діють на кожний електрон у стані динамічної рів­новаги 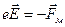. Звідси

. (6.1)

На кінцях провідника АВ створюється різниця потенціалів, яка є причиною виникнення струму в замкненому провідному контурі, що замикає кінці провідника АВ. Отже, у розглянутому прикладі ме­ханізм виникнення індукційного електричного струму в замкненому провідному контурі пояснюється на основі дії сили Лоренца на ру­хомі в магнітному полі електричні заряди.

Припустимо, що в цьому ж досліді провідник залишають нерухо­мим, а переміщають у протилежному до v напрямі постійний магніт. При цьому в системі координат, зв'язаній із провідником АВ, заряди провідника не рухаються і на них у магнітному полі сила Лоренца не діє. Однак струм у замкненому провідному контурі виникає, що фіксують по відхиленню стрілки гальванометра. Отже, рух магніту під провідником спричиняє той самий ефект, що й рух провідника над магнітом, але фізична причина ефекту інша. Це яви­ще відкрив М. Фарадей. Розглянемо ще один дослід, в якому магнітне поле постійного маг­ніту замінили магнітним полем котушки L зі струмом (рис.6.2). Характер магнітного поля в обох дослідах є однаковим. Однак у цьому разі магнітне поле можна змінювати, регулюючи струм рео­статом R, а також можна створювати або зводити до нуля магнітне поле за допомогою вимикача S. Рухаючи провідник АВ у магнітному полі котушки або котушку зі струмом відносно провідника АВ, одержимо ті самі результати, що й у попередньому досліді. Розмістимо провідник АВ і котушку L нерухомо і будемо вмикати або вимикати струм вимикачем. У момент вмикання або вимикання струму стрілка гальванометра відхилятиметься, вказуючи на виникнення в замкне­ному провідному контурі з гальванометром короткочасних імпульсів струму. Через деякий час після вмикання струму в котушці L стрілка гальванометра повертається в нульове положення, струм зникає. З цього можна зробити висновок, що індукційний струм у замкнено­му провідному контурі виникає лише в момент зміни магнітного по­ля, яке пронизує контур. У цьому можна переконатися, якщо зміню­вати струм у котушці L.

Отже, відкриття М. Фарадея полягало в тому, що індукційний струм у замкненому контурі може виникнути під час руху провідного контуру в полі магніту, під час руху магніту відносно замкненого провідного контуру і під час зміни струму в котушці, яка створює магнітне поле. Все це зводиться до одного загального правила: індукційний струм у замкненому провідному контурі виникає кожного разу при зміні магнітного потоку, який пронизує провідний контур. Щоб електричні заряди (електрони в провіднику) прийшли в на­прямлений рух, на них має діяти електрична стороння сила, спричи­нена E_{с т}, яка виникає там, де змінюється магнітне поле. Експеримен­тальні спостереження М. Фарадея сприяли відкриттю нового з а к он у про зв'язок електричного і магнітного полів: у тих областях, де змінюється магнітне поле, виникає електричне поле. Саме це елек­тричне поле спричиняє напрямлений рух електронів у провідному контурі, тобто зумовлює виникнення електрорушійної сили при всякій зміні магнітного потоку.

6.2. Електрорушійна сила індукції. Закон електромагнітної індукції Фарадея. Правило Ленца

Визначимо електрорушійну силу індукції ε _i. За означенням елек­трорушійна сила дорівнює роботі сторонніх сил при переміщенні одиничного пробного електричного заряду (q=1) по замкненому контуру. Якщо за замкнений контур L взяти контур довільного про­відника в змінному магнітному полі, то можна записати

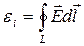, (6.2)

де Е — напруженість електричного поля, яке виникає при всякій зміні магнітного поля, що перетинає витки замкненого провідного контуру; 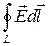— циркуляція вектора Е вздовж провідного контуру, яка дорівнює електрорушійній силі індукції. На основі (6.1) перепишемо (6.2) так:

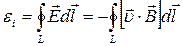. (6.3)

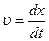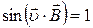У випадку, коли провідник l перемістився на малу відстань dх, у межах якої можна вважати В = const, з врахуванням того, що при і 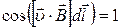, одержимо

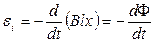, (6.4)

де d(ВІх) — зміна магнітного потоку, який пронизує замкнений про­відний контур при переміщенні провідника l на відстань dх.

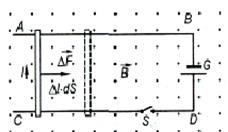Вираз (6.4) називають законом електромагнітної індукції Фарадея. У СІ коефіцієнт при 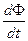дорівнює одиниці, а в системі Гауса цей коефіцієнт 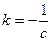. Знак мінус у правій частині рівності (6.4) визначає напрям індукційного струму відповідно до правила Ленца.

Рис. 6.3

Формулу для обчислення ЕРС індукції (6.4) можна також вста­новити на основі закону збереження енергії.

На основі означення магнітного потоку 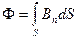і формули (6.2) вираз (6.6) можна записати в найбільш загальному вигляді, якого надав цій рівності вперше Дж. Максвел:

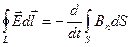, (6.7)

де L — довільний замкнений контур; S — довільна поверхня, яка спирається на контур L.

Закон, який описується співвідношенням (6.7), називають ос­новним законом електромагнітної індукції Фарадея: при всякій зміні в часі потоку магнітного поля в точках простору, де є така зміна, збуджується вихрове електричне поле, циркуляція напру­женості Е якого по довільному замкненому контуру L дорівнює швид­кості зміни потоку магнітної індукції крізь довільну поверхню S, яка спирається на контур L. Електричне поле Е, що виникає під дією змінного магнітного поля, відрізняється від електростатичного поля. Справді, з (6.7) видно, що 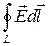в загальному випадку не дорівнює нулеві. Таке електричне поле називають вихровим, на противагу по­тенціальному електростатичному полю нерухомих зарядів, для якого завжди .

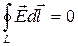Рівність (6.7) є інтегральною формою запису закону електромагнітної індукції. Запишемо цей закон у диференціальній формі. Для цього до лівої частини рівності (6.7) застосуємо теорему Стокса

.

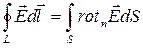Тоді

.

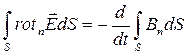Оскільки контур інтегрування L і поверхня S, що на нього спи­рається, обираються довільно, то можна записати

.

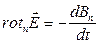Напрям проектування на нормаль п також має бути довільним. Тому від рівності проекцій перейдемо до рівності векторів

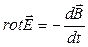
Загалом В є функцією координат і часу. Тому зміну за часом 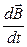правильніше буде записати як частинну похідну 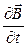. Тоді

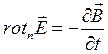. (6.8)

Рівняння (6.8) є диференціальною формою запису закону електро­магнітної індукції Фарадея. Воно описує закон виникнення вихрово­го електричного поля в певній точці внаслідок зміни індукції маг­нітного поля в тій самій точці.

Рис. 6.4

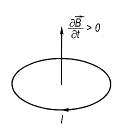
Досліди Фарадея свідчили про те, що напрям індукційного струму в замкненому провідному контурі залежить від характеру зміни маг­нітного потоку. Найбільш загальне правило для визначення напряму індукційного струму запропонував у 1833 р. Е. Ленц: індукційний струм у замкненому провідному контурі має та­кий напрям, що створюване ним власне магнітне поле протидіє змінам магнітного поля, яке збуджує індукційний струм. На рис. 6.4 показано напрям індукційного струму в контурі, коли магнітний потік, що його пронизу є, наростає. При спаданні магнітного потоку напрям індукційного струму зміниться на протилежний.

В окремому випадку руху прямого провідника перпендикулярно до ліній індукції зовнішнього магнітного поля напрям індукційного струму зруч­но визначати за правилом правої руки: якщо праву руку розмістити так, щоб лінії індукції магнітного поля входили в долоню, а відставлений під прямим кутом великий палець збігався з напрямом переміщення про­відника, то чотири випрямлені пальці вкажуть напрям індукційного струму в провіднику.

Електромагнітна індукція лежить в основі роботи генераторів, трансформаторів, коливального контуру, електромагнітів тощо.

6.3. Вихрові струми. Скін-ефект

Рис. 6.5 Рис.6.6

У масивних провідниках зі зміною магнітного потоку, що їх пронизує, індукуються замкнені електричні струми, які називають вихровими або струмами Фуко. Фізична природа цих струмів така сама, як і довільних індукційних струмів. Вихрові струми ви­никають або під час руху масивних провідників у магнітному полі, або при розміщенні їх у змінних магнітних полях. Ці струми замикаються безпосередньо в об'ємі провідника у вигляді вихороподібних замкнених ліній. За правилом Ленца вихрові струми напрямлені так, що їхнє магнітне поле протидіє змінам потоку магнітної індукції, який спричинив ви­никнення вихрових струмів. Це можна спостерігати, наприклад, під час руху магніту над провідною поверхнею. При цьому вихрові струми створюють галь­мівну силу, пропорційну швидкості ру­ху, подібно до механічних в'язких сил. Наочно продемонструвати дію вихрових струмів можна за допомогою маятника (рис. 6.5) із товстого листового алю­мінію. Поки обмотки електромагніту не з'єднані з джерелом струму), доти магнітного поля між його полюсами не­має, і маятник може вільно коливатись досить довгий час. Якщо увімкнути струм, то між полюсами електромагніту виникає магнітне поле, яке під час руху маятника індукує в його об'ємі вихрові струми, що спричиняє, за правилом Ленца, виникнення гальмівних сил, і коливання маятника швидко затухають. Якщо суцільний маятник замінитигребінчастим, то ефект вихрових струмів зменшується і такий маятник буде коливатись значно довший час.

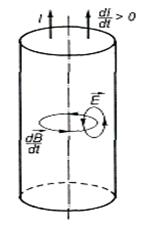
Струми Фуко в одних випадках відіграють корисну роль, в інших — шкідливу. Відповідно в першому випадку їх намагаються збільшити, у другому — зменшити. Корисну роль відіграють вихрові струми в роторах асинхронних електричних двигунів, оскільки в основі їхнього принципу роботи лежить явище виникнення струмів Фуко. Використовуючи змінні магнітні поля, можна зумовити появу знач­них вихрових струмів і за допомогою їх нагрівати або й плавити ме­тали. В окремих випадках цей спосіб зручніший порівняно з інши­ми. Разом з тим в осердях електромагнітів, трансформаторів, інших електротехнічних пристроїв виникнення значних вихрових струмів є шкідливим, оскільки призводить до їхнього перегрівання, втрати електричної енергії. У цих випадках намагаються зменшити вихрові струми переважно способом набору осердь з окремих тонких плас­тинок магнітного матеріалу, ізольованих одна від одної діелектриком, Одним із проявів електромагнітної індукції є явище скін-ефекту. Постійний струм в однорідному провіднику розподіляється рівно­мірно по площі поперечного перерізу. Під час проходження по про­віднику змінного струму в його об'ємі виникають вихрові струми, що спричиняє підсилення струму біля поверхні провідника і послаблення вздовж центральної осі. Явище концентрації змінного струму в поверхневому шарі провідни­ка називають скін-ефектом. Розглянемо механізм виникнення скін-ефекту. Візьмемо циліндричний провідник зі струмом (рис. 6.6). Усередині провідника і навколо нього виникає магнітне поле, лінії індукції якого яв­ляють собою замкнені кола з центрами на осі провідника. Зі збільшенням струму 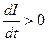наростає з часом й індукція магнітного поля В. За законом електромагнітної індукції (6.8) зміна в часі магнітного поля зумовлює виникнення вихрового елек­тричного поля, силові лінії напруженості якого є замкненими і лежать у площині, пер­пендикулярній до площини ліній магнітного поля. Біля поверхні провідника напрям напруженості вихрового електричного поля збігається з напрямом напруженості елек­тричного поля струму, а біля осі ці вектори напрямлені протилежно. Внаслідок цього густина струму біля поверхні провідника збільшується, а вздовж осі — зменшується. Виникає скін-ефект. Товщина шару провідника, в якому концентрується змінний струм, значною мірою залежить від частоти струму.

6.4. Явище самоіндукції. Індуктивність

За законом Фарадея (6.6) електрорушійна сила індукції виникає при будь-яких змінах у часі магнітного потоку Ф крізь поверхню, яка охоплюється провідним контуром. Навколо провідника зі струмом завжди виникає магнітне поле, яке створює певний потік крізь влас­ний контур провідника. При зміні струму в провіднику змінюється потік магнітної індукції. Тому в провідному замкненому контурі, в якому змінюється струм, виникає додатковий, індукційний струм. Явище виникнення індукційного струму в провіднику внаслідок зміни магнітного потоку, зумовленої зміною струму в цьому ж про­віднику, називають самоіндукцією. Явище самоіндукції є окремим випадком загального явища електромагнітної індукції. За правилом Ленца струм самоіндукції завжди напрямлений так, що протидіє змінам сили струму, який викликає самоіндукцію. Іншими словами, якщо струм у провіднику наростає, то струм самоіндукції напрямле­ний проти нього і протидіє цьому наростанню; якщо ж струм спадає, то напрям струму самоіндукції збігається з напрямом основного струму і протидіє його спаданню. Оскільки довільний провідник має самоіндукцію, то струм у кожному з них має інерцію щодо своєї зміни. Самоіндукція протидіє змінам струму в провідниках.

Індукція магнітного поля струму відповідно до закону Біо-Савара-Лапласа прямо пропорційна першому степеню сили струму. То­му й потік магнітної індукції Ф крізь певну фіксовану поверхню буде також пропорційним силі струму, тобто

Ф = LI, (6.9)

де L — коефіцієнт пропорційності, який не залежить від сили струму й індукції магнітного поля, а є однозначною характеристикою про­відного контуру, його називають індуктивністю контуру. Індук­тивність залежить від форми і розмірів контуру, а також від маг­нітних властивостей навколишнього середовища.

Закон електромагнітної індукції Фарадея для явища самоіндукції з урахуванням (6.9) запишеться так:

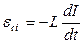. (6.10)

Одиниці вимірювання L вСІ – Гн („ Генрі ”).

.

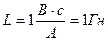За одиницю індуктивності 1 Гн взято індуктивність такого про­відника, в якому при зміні струму силою 1 А за 1 с виникає ЕРС са­моіндукції 1 В. У системі одиниць Гауса індуктивність вимірюють у сантиметрах: 1 Гн = 10⁹см.

Якщо навколишнє середовище не є феромагнітним і контур не деформується, то L=const. Інерційність зміни струмів в електрич­них колах внаслідок явища самоіндукції особливо проявляється у ви­никненні так званих екстраструмів розмикання і замикання. Індук­тивність контуру є мірою його інерції щодо зміни струму.

6.5. Струми при замиканні та розмиканні кола

За правилом Ленца додаткові струми, що виникають внаслідок самоіндукції, завжди направлені так, щоб протидіяти змінам струми в колі. Це призводить до того, що встановленні струму при замиканні кола та зникнення струму при розмиканні кола відбувається не миттєво, а поступово.

Знайдемо спочатку характер зміни струму при розмикання кола. Нехай в коло з незалежною від сили струму І індуктивністю L і опором R ввімкнено джерело струму ЕРС ε. У колі буде протікати постійний струм

(6.11)

(опір джерела вважаємо нехтовно малим). В момент часу t=0 вимкнемо джерело струму, замкнувши одночасно накоротко перемикачем П (рис. 6.7). Як тільки сила струму в колі почне зменшуватися, виникне ЕРС самоіндукції, яка протидіє цьому зменшенню. Сила струму в колі буде задовольняти рівняння

,

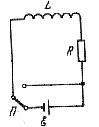
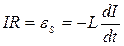або

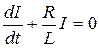. (6.12)

Розв’язавши рівняння, отримаємо:

Рис. 6.7 .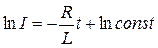

Потенціювання цього відношення дає

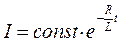. (6.13)

Вираз (6.13) є загальним розв’язком рівняння (6.12). Значення const знайдемо з початкових умов. При t=0 сила струму мала значення (6.11). Отже const=I₀. Підставивши це значення в (6.13), прийдемо до виразу

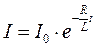. (6.14)

Отже, після відключення джерела ЕРС сила струму в колі не обертається миттєво в нуль, а зменшується поступово по експоненціальному закону (6.14). Швидкість зменшення сили стуму визначається величиною

, (6.15)

яку називають постійною часу кола. Замінивши в (6.14), отримаємо

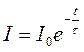. (6.16)

Згідно з цією формулою τ – це час, протягом якого сила струму зменшується в е разів. З (6.15) видно, що чим більша індуктивність кола L і чим менше його опір R, тим більша постійна часу τ і тим повільніше зменшується струм в колі.

Для спрощення розрахунків ми вважали, що коло в момент відключення джерела струму замикається накоротко. Якщо просто розірвати коло з великою індуктивністю, висока індукована напруга, що виникає, створює іскру чи дугу в місці розриву.

Тепер розглянемо випадок замикання кола. Після підключення джерела ЕРС, до тих пір, поки сила струму не досягне встановленого значення (6.11), в колі окрім ЕРС ε буде діяти ЕРС самоіндукції. Звідки, у відповідності з законом Ома

,

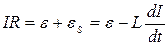або

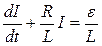. (6.17)

Прийшли до лінійного неоднорідного диференціального рівняння, яке відрізняється від рівняння (6.12) лише правою частиною. Загальним розв’язком цього рівняння буде функція

.

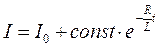В початковий момент часу сила струму І дорівнює нулю. Звідси const=-I₀. Таким чином,

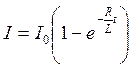. (6.18)

Ця функція описує наростання струму в колі після підключення до неї джерела струму ЕРС.

6.5. Взаємна індукція

Якщо розмістити провідні контури чи котушки зі струмами так, що магнітні потоки кожної з них хоча б частково перетинають витки сусідніх, то між ними виникає взаємна індукція. При цьому ЕРС у кожному контурі виникає не тільки внаслідок зміни потоку індук­ції магнітного поля, створюваного струмом цього самого контуру (явище самоіндукції), а й завдяки зміні потоку індукції магнітного поля, створюваного струмами сусідніх контурів (явище взаємної індукції). У таких випадках кажуть, що контури мають індуктивний зв'язок. Явище взаємної індукції полягає в наведенні ЕРС індукції в провідниках, які містяться поблизу інших провідників, струми яких змінюються з часом.

Розглянемо дві індуктивно зв'язані котушки зі струмами силою І₁ і І₂, які мають відповідно N₁ і N₂ витків і коефіцієнти індуктивності L₁₁ і L₂₂ (рис. 6.8). Повний потік, що охоплюється витками першої котушки,

Ф₁ =Ф₁₁ +Ф₁₂, (6.19)

де Ф₁₁ — магнітний потік крізь першу котушку, створюваний стру­мом силою І₁; Ф₁₂ — та частина магнітного потоку, створювана стру­мом силою I₂, яка охоплюється витками першої котушки. Аналогічно повний потік, що пронизує витки другої котушки,

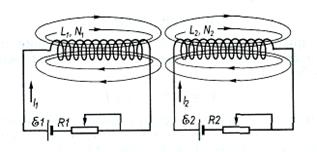Ф₂=Ф₂₂ + Ф₂₁. (6.20)

Рис.6.8

Магнітні потоки кожної котушки пропорційні силам струмів

Ф₁₁ = L₁₁ I₁; Ф₂₂ = L₂₂ I₂.

Та частина магнітного потоку Ф₁₂, яка охоплюється витками першої котушки, створюється завдяки магнітному полю струму силою I₂ у другій котушці. Тому ця частина потоку пропорційна силі струму I₂, тобто Ф₁₂ = L₁₂I₁, де L₁₂ — коефіцієнт взаємної індукції першої ко­тушки. Аналогічно для другої котушки Ф₂₁ = L₂₁ I₁. Тоді рівності (6.19) і (6.20) перепишемо так:

Ф₁ = L₁₁ I₁+ L₁₂ I₂; Ф₂ = L₂₂ I₂+ L₂₁ I₁.

Відповідно ЕРС індукції, що виникають у котушках, будуть

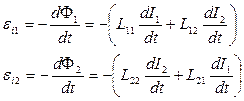(6.21)

На основі теореми взаємності, яка встановлює перехресний зв'язок між двома джерелами струму і створюваними ними полями в місцях розміщення джерел для тієї самої замкненої лінійної системи у не феромагнітних середовищах, можна стверджувати рівність коефіцієнтів взаємоіндукції для довільних двох контурів

L₁₂=L₂₁. (6.22)

Доведемо це для випадку двох індуктивно зв'язаних контурів, по яких проходять струми силою I₁ та I₂. Припустимо, що контур, в якому протікає струм силою I₁ нерухомий, а контур, в якому про­тікає струм силою I₂, переміщається з нескінченності в задане поло­ження. При цьому магнітний потік крізь другий контур, створюва­ний струмом у першому контурі, змінюватиметься від нуля до Ф ₁₂, а робота з його переміщення

А₁= І₁Ф₁₂ = L₁₂I₁I₂.

Якщо другий контур буде нерухомим, а перший переміщати­меться з нескінченності в задане положення, то відповідно буде ви­конана робота

А₂= І₂Ф₂₁ = L₂₁I₁I₂.

У кожному цих випадків робота є мірою взаємної енергії контурів зі струмами і її значення не залежить від того, який з кон­турів переміщався. Отже, А₁ = А₂, звідси L₁₂=L₂₁.

Коефіцієнти взаємоіндукції є мірою магнітного зв'язку між кон­турами і залежать від геометричної форми, розмірів і взаємного роз­міщення контурів зі струмом, а також від магнітних властивостей се­редовища, де розміщені контури. В СІ коефіцієнти взаємної індукції, як і самоіндукції, вимірюють у генрі. Розрахунки коефіцієнтів взаємної індукції є досить складними. Найпростіше це можна здійснити для тороїду, що має дві одношарові котушки, які щільно прилягають одна до одної. У цьому разі коефіцієнт взаємної індукції можна визначити за формулою

,

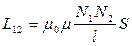де N₁ і N₂ — відповідно кількість витків першої і другої котушок.

6.6. Енергія магнітного поля струму. Енергія і густина енергії магнітного поля

Електричний струм у провідниках одержують завдяки енергії сто­ронніх джерел ЕРС. При проходженні в замкненому провідному контурі постійного струму його енергія витрачається на виділення джоулевого тепла і на живлення споживачів, а магнітне поле навколо провідника не змінюється. Зі зміною струму змінюються магнітне поле і його потік індукції крізь поверхню, що охоплюється про­відним контуром. Внаслідок цього в провіднику виникає ЕРС індук­ції, напрямлена за правилом Ленца завжди так, що протидіє змінам струму і магнітного потоку. При вмиканні джерела сторонніх ЕРС сила струму зростає від нуля до /. Відповідно змінюється магнітний потік і в контурі виникає ЕРС індукції, дія якої протилежна дії ЕРС джерела.

Щоб сила струму зростала, необхідно ЕРС індукції компенсувати енергією сторонніх ЕРС. Отже, у процесі зростання сили струму джерело сторонніх ЕРС виконує роботу проти ЕРС індукції. Ця ро­бота йде на створення магнітного поля, енергія якого дорівнює ро­боті сторонніх ЕРС. За час dt при силі струму I буде виконана робота

.

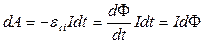Зі зміною потоку dФ пов'язана зміна енергії магнітного поля

.

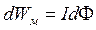Оскільки dФ = LdI, то

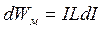. (6.23)

Інтегруючи (6.23) в межах від нуля до I, одержуємо

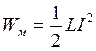. (6.24)

Формула (6.24) визначає енергію магнітного поля замкненого про­відного контуру зі струмом I та індуктивністю L.

Свідченням наявності енергії магнітного поля є виникнення екстраструмів розмикання. У цьому явищі ми маємо справу з пере­творенням енергії магнітного поля провідника з індуктивністю L в енергію струму самоіндукції. Оскільки L залежить від магнітних властивостей середовища, де локалізоване магнітне поле, то й енер­гія магнітного поля також залежить як від сили і розподілу струмів, так і від властивостей навколишнього середовища. Енергія магнітно­го поля розподілена в усьому просторі, де локалізоване поле, і фор­мула (6.24) визначає повну енергію магнітного поля струму. Однак часто важливо знати енергетичні характеристики в окремих областях чи навіть точках заданого магнітного поля. Для цього треба формулу для обчислення енергії виразити через вектори поля, які є локальни­ми характеристиками його в кожній точці. Для спрощення розгляне­мо окремий випадок магнітного поля нормального соленоїда зі стру­мом, розміщеного у вакуумі. Індуктивність соленоїда 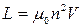. Рівність (6.24) перепишеться так:

.

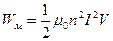Всередині соленоїда магнітне поле є однорідним, і його індукція 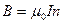. Тоді

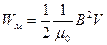. (6.25)

Якщо врахувати, що В = 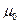H, де H — вектор напруженості маг­нітного поля, то формула (6.25) матиме такий вигляд:

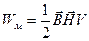. (6.26)

Енергія магнітного поля розподілена в просторі навколо провідника з об'ємною густиною

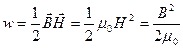. (6.27)

Отже, об'ємна густина енергії магнітного поля в полі кожної точки простору визначається значеннями векторів поля в цій точці.