Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Магнітне поле і його характеристики

1.1 Магнітне поле

У 1820 році Ерстед встановив, що рухомі заряди взаємодіють не так як ті, що перебувають в стані спокою. У 1901 році Ейхенвальд показав, що коли заряджене тіло перебуває в спокої відносно спостерігача навколо нього існує електричне поле, а якщо почне тіло рухатися, то виникає магнітне поле.. Щоб виявити його наявність потрібно розмістити біля рухомого тіла магнітну стрілку і вона буде відхилятися на певний кут.

Ампер встановив, що будь-який електричний струм здатен взаємодіяти з іншим струмом з силою, яку неможливо пояснити кулонівською взаємодією. Згідно з теорією близькодії нерухомі електричні заряди взаємодіють через електричне поле.

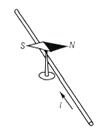
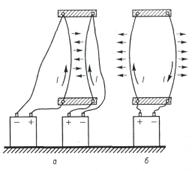Провідники зі струмом є електрично нейтральними, але якщо пропустити струм по двох паралельних провідниках, то вони будуть притягуватися або відштовхуватись.

Рис.1.1 Рис.1.2

Взаємодію між провідниками зі струмом (між рухомими електричними зарядами) називають магнітною взаємодією, а сили, з якими вони діють один на одного – магнітними силами.

Причиною магнітних взаємодій є магнітне поле – особлива форма матерії, через яку взаємодіють рухомі заряджені частинки, або тіла, які мають магнітний момент. Експериментальним доведенням існування магнітного поля є існування електромагнітних хвиль. Магнітне поле є окремим проявом електромагнітного поля.

Нерухомі заряди не створюють магнітного поля, його утворюють лише електричний струм і постійні магніти. При вивченні взаємодії постійних магнітів було встановлено, що постійні магніти мають два полюси (північний і південний), однойменні полюси відштовхуються, а різнойменні притягуються. Це може привести до думки, що в природі можуть існувати магнітні заряди. Проте, якщо постійний магніт поділити на дві частини, то кожна частина все одно буде мати два полюси. Не може існувати магніт з одним полюсом.

Якщо окремі тіла можна зарядити позитивно або негативно, оскільки існує елементарний заряд, то ніколи не можна відокремити північний полюс магніту від південного. Отже, згідно з гіпотезою про елементарні магнітні струми Ампера, магнітні заряди в природі не існують. Всередині атомів і молекул циркулюють елементарні електричні струми. Якщо вони розміщені хаотично, то їх дія взаємно компенсується і магнітних властивостей тіло не має.

В намагніченому стані елементарні струми орієнтовані. Тоді магнітні властивості тіла пояснюються замкненими електричним струмами всередині нього. Таким чином, магнітна взаємодія – це взаємодія електричних струмів.

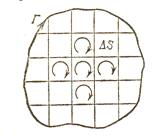Щоб дослідити властивості магнітного поля використовують маленьку плоску рамку зі струмом, підвідні проводи до якої скручують так, щоб в них проходив той самий електричний струм, але в протилежних напрямах. Тому сили магнітного поля, які діють на проводи однакові, але протилежно направлені.

Рис.1.3

Розміри рамки і сила струму мають бути такими, щоб магнітне поле самої рамки не спотворювало досліджуване поле. Таку рамку називають пробним контуром.

Розмістимо провідник біля пробного контуру. Якщо струму в провіднику немає, рамка перебуває в стані байдужої рівноваги. Якщо струм є, то рамка повернеться так, щоб провідник опинився в площині рамки. Якщо змінити напрям струму в провіднику рамка повернеться на 180^о. Тобто магнітне поле чинить орієнтуючу дію на пробний контур.

Пробний контур в магнітному полі зазнає дії обертального моменту сили М. Для певної точки магнітного поля максимальне значення обертального моменту дорівнює добутку сили струму, який протікає в контурі, на площу контуру.

.

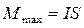Величину р_с, що характеризує магнітні властивості контуру, називають магнітним моментом контуру. Він визначає поводження контуру в зовнішньому магнітному полі.

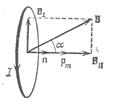Рис.1.4 .

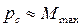Магнітний момент контуру – векторна величина. Напрям вектора збігається з напрямом вектора позитивної нормалі n до площини контуру.

Додатній напрям нормалі збігається з напрямом переміщення правогвинтового свердлика, який обертається в напрямі протікання струму. Напрям вектора магнітного моменту показує північний полюс магнітної стрілки.

1.2. Індукція магнітного поля

Відношення максимального магнітного моменту, що діє на контур до магнітного моменту самого контуру не залежить від властивостей пробного контуру і може бути характеристикою магнітного поля:

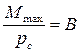, (1.1)

де В – магнітна індукція поля. Рівність (1.1) дозволяє визначити лише модуль магнітної індукції. Напрям вектора В збігається з напрямом зовнішнього магнітного поля.

Магнітна індукція – силова характеристика магнітного поля в даній точці простору. В загальному випадку В залежність магнітного моменту від орієнтації контуру в просторі визначається за правилом векторного добутку.

,

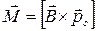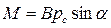, (1.2)

де α – кут між векторами магнітної індукції і магнітного моменту.

З формули (1.2) видно, що максимальне значення обертального моменту досягається при α =π /2 рад.

Рівновага контуру в магнітному полі можлива, коли В і р_с направлені по одній прямій.

В системі СІ одиниці вимірювання магнітної індукції – Тл („тесла”).

1 Тл – це індукція магнітного поля, при якій на контур площею 1 м² зі струмом 1 А діє обертальний момент 1 Н∙ м.

Лінії магнітної індукції – лінії, дотичні до яких в даній точці збігаються за напрямом з вектором В в цій точці.

Лінії магнітної індукції завжди замкнені і завжди охоплюють провідники зі струмом. Такі магнітні поля називають вихровими. Напрям ліній магнітної індукції пов’язаний з напрямом протікання струму правилом правого гвинта.

Магнітне поле називається однорідним, якщо в усіх точках поля магнітна індукція однакова:

.

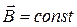Лінії магнітної індукції однорідного поля паралельні, їх густина однакова в усіх точках поля. Густиною ліній магнітної індукції характеризують значення магнітної індукції. Через одиничну площину, перпендикулярну лініям магнітної індукції проводять таке число ліній, що дорівнює або пропорційне модулю магнітної індукції в цій області магнітного поля.

1.3. Закон Біо-Савара-Лапласа

Для магнітного поля справедливий принцип суперпозиції:

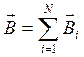. (1.3)

Розглянемо магнітні поля, створені постійними електричними струмами.

Заряд Q, який рухається з постійною швидкістю V створює магнітне поле індукцією В (рис.1.5):

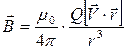, (1.4)

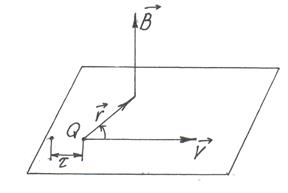де μ ₀ – магнітна стала (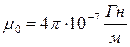), r – радіус-вектор від заряду до точки спостереження. Кінець радіус-вектора нерухомий в даній системі відліку, а початок рухається зі швидкість V. Тому магнітна індукція залежить не лише від положення точки спостереження, а

і від часу: .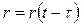

Рис. 1.5

За формулою (1.4) вектор магнітної індукції направлений перпендикулярно до площини, в якій розташовані вектори і 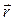, причому обертання навколо 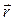в напрямі 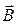утворює з напрямом правогвинтову систему.

Нехай заряд рівномірно розподілено по поверхні з поверхневою густиною 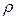, тоді

.

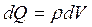Врахуємо, що і підставимо значення заряду в формулу (1.4), тоді вона набуде вигляду (1.5):

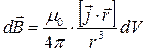. (1.5)

Якщо струм тече по тонкому провіднику, в якому площа поперечного перерізу 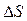, то

,

де dl – елемент довжини провідника.

Введемо вектор 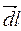в напрямі протікання струму І. Тоді

, (1.6)

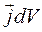– об’ємний елемент струму, 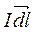– лінійний елемент струму.

Замінимо в формулі (1.5) об’ємний елемент струму лінійним:

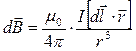. (1.7)

Формули (1.5) і (1.7) є математичними записами закону Біо-Савара-Лапласа. Для знаходження магнітної індукції поля в даній точці, за принципом суперпозиції про інтегруємо (1.5) або (1.7):

. (1.8)

Розрахунок спрощується, якщо розподіл струму має певну симетрію.

1.4. Магнітне поле прямого струму

Використаємо формулу (1.7). В точці А вектори dB всіх струмів мають однаковий напрям, тому складання векторів замінюємо складанням їх модулів.

; ;

;

.

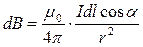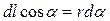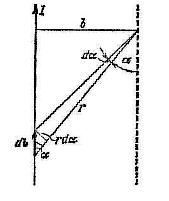
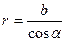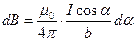Інтегруючи за всіма елементами струму (від – π /2 до +π /2), отримаємо:

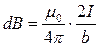. (1.9)

Рис.1.6

1.5. Магнітне поле на осі колового струму

Вектор 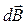елемента струму 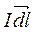від всіх струмів буде утворювати „конус” і таким чином результуючий вектор 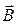направлений по осі z.

,

.

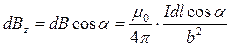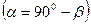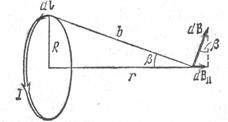В цій формулі вже враховано, що кут між dB і Idl становить π /2.

Проінтегруємо по всім ділянкам dl (2π R), врахувавши що 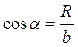, 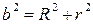. Тоді отримаємо:

Рис.1.7 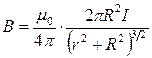. (1.10)

Звідси слідує, що в центрі витка з струмом (r=0) і на відстані 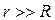модуль вектора магнітної індукції визначається за формулами відповідно:

,

.
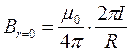
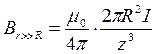