💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Магнітне поле в магнетиках

4.1. Намагнічування магнетиків. Опис магнітного поля в магнетиках

Якщо магнітне поле, утворене струмами провідника внести в ту чи іншу речовину, то магнітне поле зміниться. Отже будь-яка речовина є магнетиком, тобто може під дією магнітного поля набувати магнітного моменту, тобто намагнічуватись.

Намагнічена речовина створює магнітне поле індукцією 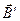, яке разом з первинним полем індукцією 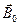обумовлене струмами провідності. В сумі ці два поля створюють загальне магнітне поле

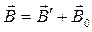(4.1)

(значення 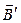і 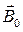усереднені по фізично нескінченно малому об’єму V). Поле 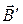і 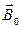струмів провідності не має джерел (магнітних зарядів) і тому для поля 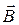при наявності магнетика справедлива теорема Гауса. Це означає, що лінії магнітної індукції 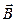і при наявності речовини залишаються неперервними:

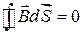. (4.2)

Для пояснення процесу намагнічування Ампер запропонував ідею, що в молекулах речовини циркулюють колові струми (молекулярні струми). Кожен такий струм володіє магнітним моментом і створює в навколишньому середовищі просторове магнітне поле. При відсутності зовнішнього магнітного поля ці молекулярні струми орієнтовані хаотично, внаслідок чого обумовлене ними результуюче поле дорівнює нулю.

В силу хаотичної орієнтації магнітних моментів окремих молекул сумарний магнітний момент тіла буде дорівнювати нулю. Під дією зовнішнього поля магнітні моменти молекул набувають певної орієнтації в одному напрямі і сумарний магнітний момент відмінний від нуля. Магнітні поля окремих молекулярних струмів вже не компенсують один одного і виникає поле .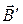

Рис.4.1

Оскільки рух електронів аналогічний коловому струму, то виникає магнітне поле і рух електронів можна характеризувати орбітальним моментом.

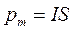. (4.3)

Сумарний орбітальний момент дорівнює векторній сумі орбітальних моментів окремих атомів, що входять в речовину.

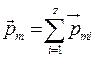(4.4)

Якщо речовина має молекулярну будову, то орбітальний момент дорівнює векторній сумі орбітальних моментів атомів, що входять до складу молекули.

Незалежно від орбітального руху, електрон є джерелом магнітного поля, оскільки він має власний момент імпульсу, який називається спіном.

Отже, магнетизм атомів зумовлений:

- рухом електронів по орбітах навколо ядра;

- спіном електронів.

Намагніченість магнетика характеризується магнітним моментом одиниці об’єму – намагніченістю J.

Якщо магнетик намагнічений неоднорідно, то

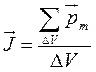, (4.5)

де 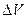– фізично нескінченно малий об’єм, взятий в межах розглядуваної точки, p_m – магнітний момент окремої молекули. Сумування проводиться по всім молекулам, охопленим об’ємом .

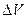Поле 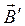не має джерел, тому дивергенція вектора магнітної індукції результуючого поля дорівнює нулю.

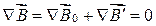
4.2. Напруженість магнітного поля

Запишемо вираз для ротора результуючого поля (4.1):

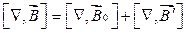
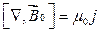(), де j – густина макроскопічних струмів.

Аналогічно ротор індукції молекулярного поля пропорційний густині молекулярних струмів:

,

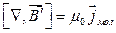тоді ротор результуючого поля:

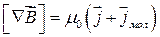. (4.6)

З цього слідує, що при розрахунках поля в магнетиках, стикаємось з такими ж проблемами, як і при визначенні електричного поля в діелектриках (необхідно знайти густину не лише макроскопічних струмів, а і молекулярних). Густина молекулярних струмів залежить від індукції магнітного поля.

Щоб встановити вигляд допоміжної величини виразимо густину молекулярних струмів через намагніченість.

Обчислимо суму струмів, охоплених контуром Г:

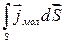, (4.7)

d 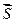– поверхня, натягнута на контур Г.

В алгебраїчну суму молекулярних струмів, охоплених контуром входять лише ті, що нанизані на даний контур.

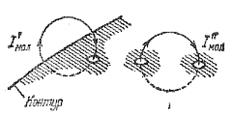Молекулярні струми, не нанизані на поверхню або не перетинають дану поверхню, або перетинають її два рази і в результаті сила струму дорівнює нулю і залишаються лише струми, нанизані на контур.

Рис. 4.2

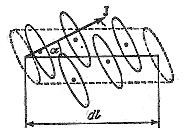Об’єм даного циліндра чисельно дорівнює 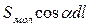, де S – площа, охоплена окремим молекулярним струмом. Якщо n – концентрація, то сумарний струм, охоплений елементом dl буде дорівнювати 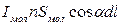. Добуток молекулярного струму на молекулярну площу дорівнює магнітному моменту окремого молекулярного струму:

.

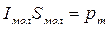Тобто, добуток 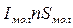є магнітним моментом одиниці об’єму, а це є намагніченістю за означенням: Рис.4.3

,

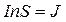а вся величина з 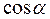є проекцією вектора намагніченості на напрям елемента .

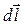Таким чином, сумарний молекулярний струм, охоплений :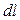

,

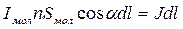а сума молекулярних струмів, охоплених всім контуром згідно рівняння (4.7):

.

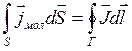Перетворимо праву частину цього рівняння за правилом Стокса:

.

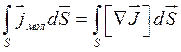Це рівняння повинно виконуватися при довільному виборі поверхні S, а це можливо лише у тому випадку, коли підінтегральні вирази рівні в кожній точці магнетика.

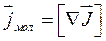. (4.8)

Тобто густина молекулярних струмів визначається ротором вектора намагніченості. Якщо ротор дорівнює нулю, молекулярні струми орієнтовані так, що їх сума в середньому дорівнює нулю.

Підставимо рівняння (4.8) у формулу (4.6) і тоді отримаємо:

.

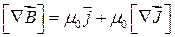Якщо розділимо дане співвідношення на магнітну сталу і об’єднаємо разом ротори, то:

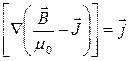. (4.9)

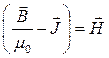. (4.10)

Рівняння (4.10) виражає ту допоміжну величину, ротор якої визначається одними лише молекулярними струмами. Ця величина називається напруженістю магнітного поля і за формулою (4.9)

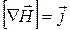. (4.11)

Тобто ротор вектора напруженості магнітного поля чисельно дорівнює величині макроскопічних струмів.

Візьмемо контур Г. Тоді

.

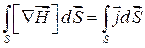І з теореми Стокса, перетворивши ліву частину отримаємо:

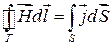. (4.12)

Якщо макроструми течуть по провідникам, що охоплені контуром, рівняння (4.12) можна записати у вигляді:

.

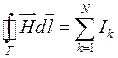Рівняння (4.11) та (4.12) є математичними записами теореми про циркуляцію вектора напруженості магнітного поля.

Напруженість магнітного поля 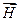є аналогом електричного зміщення 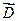, а індукція є аналогом напруженості .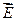

Магнітне та електричне поля мають різну природу (електричне поле потенціальне, а магнітне – соленоїдальне), тому вектори і 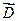мають більше подібностей в своїй поведінці.

Так як величина намагніченості у вакуумі 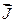=0, то напруженість поля у вакуумі чисельно дорівнює:

.

Одиниці вимірювання напруженості в системі СІ – А/м.

Намагніченість зв’язана не з магнітною індукцією, а з напруженістю магнітного поля і вважають, що в кожній точці магнетика

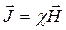, (4.14)

де 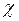– магнітна сприйнятливість, величина характерна для кожного магнетика.

Досліди показують, що для не феромагнітних речовин при не дуже великих магнітних полях, дана величина 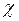не залежить від напруженості магнітного поля, тому розмірність напруженості співпадає з розмірністю намагніченості. Відповідно, магнітна сприйнятливість – величина безрозмірна.

Якщо в (4.10) підставити вираз (4.14) для намагніченості, то отримаємо:

,

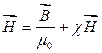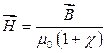, (4.15)

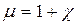, (4.16)

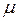– відносна магнітна проникність речовини (безрозмірна величина).

На відміну від діелектричної сприйнятливості, яка може мати лише додатні значення більші за одиницю, магнітна сприйнятливість буває як позитивною, так і негативною, тому і магнітна проникність може бути як більшою, так і меншою за одиницю.

З урахуванням рівності (4.16) формулі (4.15) можна надати вигляд:

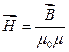(4.17)

Таким чином, напруженість магнітного поля – це вектор, який має такий же напрям як і вектор магнітної індукції, але менший на величину 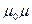по модулю.

В анізотропному середовищі вектори напруженості та магнітної індукції на співпадають за напрямком.

4.3. Умови на межі двох магнетиків

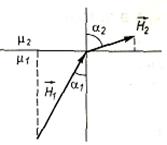Для розв'язування задач з магнітостатики в магнетиках по­трібно ще знати поведінку векторів і 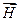на межі поділу магнетиків з різною магнітною проникністю μ, тобто граничні умови. Ці умови встановлюють так само, як і для векторів 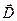і 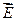електростатичного по­ля. Скориставшись рівнянням 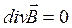і методикою виведення граничної умови для нор­мальної складової вектора 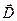, одержимо

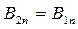. (4.18)

Отже, на межі поділу двох магнетиків нормальні складові вектора індукції В єнеперервними і, таким чином, при переході межі поділу В_п не змінюється.

Рис.4.4

Граничну умову для тангенціальної складової вектора H виведемо з рівняння 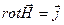. Помножимо обидві частини цього рівняння на 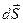, і інтегруємо по S. До лівої частини застосуємо теорему Стокса. Тоді 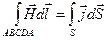, де S — поверхня, обмежена контуром АВСDА. Маємо

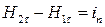, (4.19)

де і_n — лінійна густина поверхневих струмів провідності. Лінійною густиною поверхневих струмів називають такий струм, який припадає на одиницю довжини відрізка, розміщеного перпендикулярно до на­пряму струму на поверхні, по якій він проходить. Напрям i збігається з напрямом поверхневого струму, за значенням дорівнює проекції i на перпендикуляр до одиничного відрізка. Якщо і_n = 0, то .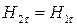

На межі поділу двох магнетиків з різними значеннями магнітних проникностей μ ₁ і μ ₂ магнітні силові лінії мають заломлюватись. Дійсно, якщо взяти плоску межу поділу (рис. 4.4) і припустити, що поверхневі струми провідності відсутні (і_n = 0), то на основі гранич­ної умови (4.19) можна записати

.

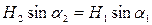Для нормальних складових вектора індукції В на основі граничної умови (4.16) та рівності (4.15)

.

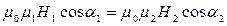З цих рівнянь знаходимо, що

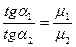. (4.20)

Переходячи з магнетика з меншою маг­нітною проникністю в магнетик з більшою магнітною проникністю (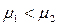), магнітні силові лінії, заломлюючись, віддаляються від нормалі до межі поділу магнетиків. Це означає, що магнітні силові лінії концентруються більше в магнети­ках з більшою магнітною проникністю