Закон повного струму

2.1. Потік і циркуляція вектора магнітної індукції.

Магнітне поле володіє двома властивостями. Ці властивості пов’язані з потоком і циркуляцією векторного поля і виражають основні закони магнітного поля.

Потік вектора В через замкнену поверхню дорівнює нулю, тобто за теоремою Гауса:

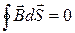. (2.1)

Дана теорема виражає, що лінії вектора магнітної індукції не мають ні початку, ні кінця, тому число ліній, які виходять з будь-якого об’єму замкненої поверхні S завжди дорівнює числу ліній, що входять в об’єм. З цього витікає, що потік вектора В крізь поверхню S, яка обмежена деяким замкненим контуром не залежить від форми поверхні S.

Рівняння (2.1) виражає також той факт, що в природі не існує магнітних зарядів, на яких би починалися або закінчувалися лінії магнітної індукції. Тобто, на відміну від електричного поля, магнітне поле не має джерел.

Теорема про циркуляцію вектора В:

Циркуляція по деякому контуру Г чисельно дорівнює добутку магнітної сталої на алгебраїчну суму сил струмів, що пронизують контур.

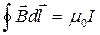, (2.2)

.

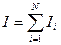І_і – величина алгебраїчна. Вважають, що І_і> 0, якщо напрям струму зв’язаний з напрямом обходу контуру правило правого гвинта. Струм протилежного напрямку негативний.

Якщо струм рівномірно розподілений по об’єму, в якому знаходиться контур Г, то

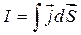. (2.3)

Густина струму j відповідає точці, де знаходиться елемент dS, причому вектор 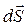утворює з напрямом обходу контуру правогвинтову систему.

В загальному вигляді рівняння (2.2):

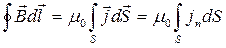. (2.4)

Так як циркуляція вектора В пропорційна силі струму, який обмежений контуром, то магнітному полю в загальному випадку не можна приписувати скалярний потенціал, який був би зв’язаний з індукцією магнітного поля, аналогічно до електричного поля (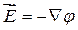). Даний потенціал був би неоднозначним. При кожному обході по контуру і поверненні в початкову точку він отримував б приріст 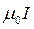, проте в тій області простору, де струмів немає магнітний потенціал 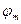вводиться і використовується.

Теорема про циркуляцію вектора В відіграє значну роль при обчисленні індукції магнітного поля. Дана теорема аналогічна до теореми Гауса для напруженості та електричного зміщення в електричному полі.

Поле вектора магнітної індукції визначається всіма струмами, а циркуляція – лише тими струмами, які пронизують контур. Але в деяких випадках, при існуванні певної симетрії, теорема про циркуляцію В є ефективною і дає змогу знаходити значення магнітної індукції (у випадках коли обчислення циркуляції можна звести до множення В на довжину контуру чи її частини).

Розглянемо тепер диференціальну форму основних законів магнітного поля.

Дивергенція поля

В магнітному полі дивергенція поля магнітної індукції дорівнює нулю:

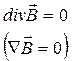(2.5)

Рівняння (2.5) є фундаментальним і справедливе не лише для постійних струмів, а і для змінних магнітних полів.

Ротор поля вектора В

Розглянемо відношення циркуляції вектора В до площі S, що обмежена даним контуром. Нехай це відношення прямує до деякої границі при :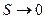

.

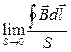Дана границя залежить від орієнтації контуру в даній точці простору. Орієнтація задається вектором нормалі n до площини контуру. Напрям її зв’язаний з напрямом обходу по контуру правилом правого гвинта.

Даний вектор, до якого прямує розглядувана величина є ротором поля вектора магнітної індукції:

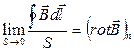, (2.6)

де 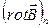– проекція вектора на нормаль n.

Згідно (2.6) рівняння (2.4) набуде вигляду:

.

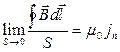Або:

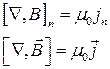(2.7)

Останнє рівняння є диференціальною формою теореми про циркуляцію вектора В.

З цього видно, що ротор В співпадає з вектором густини струму j в даній точці.

В електричному полі циркуляція вектора напруженості дорівнює нулю, тому для електричного поля справедливо:

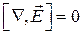. (2.8)

Векторне поле, ротор якого всюди дорівнює нулю є потенціальним. В протилежному випадку поле є соленоїдальним.

2.2. Магнітне поле соленоїда і тороїда

Соленоїд – котушка, на яку намотано довгий провідник (l> > d).

Нехай струм І тече по провіднику, який намотано на довгий циліндр (соленоїд). На одиницю довжини циліндра припадає n витків провідника.

Якщо крок даної котушки малий, то кожен виток можна приблизно замінити замкненим витком. Також вважаємо, що переріз циліндра настільки малий, що струм можна вважати таким, що тече по його поверхні.

Чим довший соленоїд, тим менша індукція ззовні нього. Магнітне поле ззовні нескінченного соленоїда відсутнє.

Рис. 2.1

З міркувань симетрії індукція всередині соленоїда направлена по його осі і складає з напрямом сили струму правогвинтову систему.

Візьмемо прямокутний контур. Тоді циркуляція магнітної індукції по контуру буде чисельно дорівнювати Bl. В такому випадку контур охоплює струм nlI.

За теоремою про циркуляцію вектора магнітної індукції

.

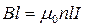Тоді всередині довгого соленоїда поле визначається за формулою:

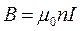. (2.9)

Поле однорідне за виключенням областей, які прилягають до торців соленоїда.

Добуток nI називають числом Ампер-витків.

Тороїд – провідник, намотаний на каркас, який має форму тора (рис.2.2).

Лінії магнітної індукції у випадку тороїда направлені по колу. В якості контуру можна взяти одне з таких кіл. Якщо контур знаходиться всередині тороїда (кола радіуса r), то він містить струм NI, де N – кількість витків, охоплених контуром.

За теоремою про циркуляцію:

.

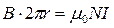Рис.2.2

І відповідно поле всередині тороїда:

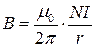. (2.10)

Таким чином, всередині тороїда магнітне поле співпадає з полем прямого струму NI, який тече по його осі.

Якщо 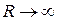при незмінному перерізі тороїда отримаємо формулу (2.9) для соленоїда.

Якщо контур знаходиться ззовні тороїда, то струмів він не охоплює, 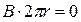. Отже ззовні тороїда поле відсутнє.

2.3. Закон Ампера

Кожен носій струму відчуває дію магнітного поля. Дія цієї сили передається провіднику, по якому рухаються заряди. В результаті магнітне поле діє з певною силою на сам провідник зі струмом. Такі висновки можна зробити із теоретичних міркувань.

Розглянемо ці явища з практичної точки зору.

Нехай об’ємна густина заряду, який є носієм струму чисельно дорівнює ρ. Виділимо елемент об’єму dV провідника. В ньому знаходиться заряд (носій струму) ρ dV. Тоді сила, що діє на елемент провідника dV, може бути записана у вигляді:

,

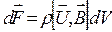де U – швидкість впорядкованого руху зарядів.

Враховуючи, що 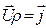, маємо

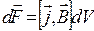. (2.11)

Якщо струм тече по тонкому провіднику, то 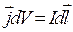. Тоді

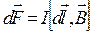, (2.12)

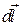– вектор, що співпадає за напрямом з струмом і характеризує елемент довжини тонкого провідника.

Рівняння (2.11) і (2.12) виражають закон Ампера. Інтегруючи ці рівняння по елементам струму (об’ємним та лінійним), отримаємо силу, яка діє на провідник. Такі сили називаються Амперовими силами.

,

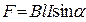α – кут між напрямом сили струму І і вектором магнітної індукції В.

Напрям сили Ампера визначають за правилом лівої руки: якщо силові лінії входять в долоню, чотири пальці вказують напрям сили струму, то великий палець, відігнутий на 90^о покаже напрям сили Ампера.

2.4. Сила Лоренца

Сила F, що діє на точковий заряд Q залежить від положення даного заряду і швидкості його руху. Відповідно силу F розділяють на дві складові – електричну F_ел (не залежить від руху) і магнітну F_м (залежить від швидкості руху).

.

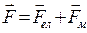В будь-якому місці поля магнітна складова цієї сили F_м перпендикулярна визначеному в даному місці напряму і модуль її пропорційний складовій швидкості, яка перпендикулярна до даного виділеного напрямку.

, (2.13)

тоді повна електромагнітна взаємодія, яка діє на заряд Q:

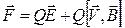. (2.14)

Дану силу називають силою Лоренца.

Рівняння (2.14) справедливе для постійних та змінних електричних і магнітних полів.

За дією сили Лоренца на заряд можна визначити модулі і напрям напруженості електричного та індукції магнітного полів, тому рівняння (2.14) можна розглядати для визначення електричних і магнітних полів.

На заряд, що знаходиться в стані спокою в магнітному полі, магнітне поле не діє.

Модуль сили Лоренца визначається за формулою:

.

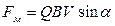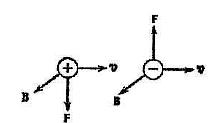
Для позитивних зарядів напрям сили Лоренца визначається за правилом лівої руки (аналогічно до сили Ампера), для негативних зарядів сила Лоренца має протилежний напрям.

Рис.2.3

Проаналізувавши останню формулу можемо зробити висновок:

- якщо V=0, то F_л=0, тобто сила Лоренца не діє на нерухомі заряди;

- якщо α =0, sin α =0, то F_л=0. Тобто якщо частинка рухається так, що вектор її швидкості паралельний вектору магнітної індукції, на неї з боку магнітного поля не діє ніяка сила.

Оскільки сила Лоренца завжди перпендикулярна швидкості руху частинки, сила Лоренца не змінює модуль швидкості, а змінює лише її напрям.

Сила Лоренца не виконує роботи.