💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Контур зі струмом в зовнішньому магнітному полі

3.1. Стан контуру зі струмом в зовнішньому магнітному полі

Розглянемо плоский контур зі струмом І в однорідному магнітному полі індукцією В. Коли контур плоский і його розміри дуже малі, він називається елементарним контуром. Результуюча сила, що діє на елементарний контур

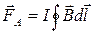. (3.1)

Даний інтеграл – замкнений ланцюг елементарних векторів 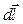і тому він чисельно дорівнює нулю. Тобто результуюча сила в однорідному магнітному полі F=0.

Поведінку елементарного контуру зі струмом можна описати за допомогою магнітного моменту .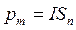

Результуючий момент сил Ампера:

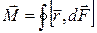. (3.2)

Але для будь-якої вільної форми контуру зі струмом магнітний момент можна представити як добуток:

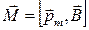. (3.3)

Таким чином, за правилом векторного добутку, момент сил Ампера, що діють на контур в однорідному полі перпендикулярний до вектора магнітного моменту і вектора В.

Тоді можемо записати модуль даного вектора:

,

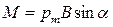де α – кут між векторами p_m і B.

Якщо вектори магнітного моменту та індукції магнітного поля сонаправлені, то момент сил Ампера дорівнює нулю і положення контуру стійке. Якщо ці вектори протилежно направлені, то положення контуру нестійке.

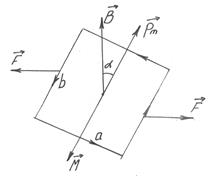
Сили, що діють на сторони а контуру перпендикулярні до даних сторін і вектора магнітної індукції В (рис.3.1).

Рис.3.1

Сторони b перпендикулярні вектору магнітної індукції, тому на них діють сили Ампера:

.

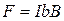Ці сили прагнуть повернути контур так, щоб його вектор магнітного моменту став паралельним В. Тобто на контур діє пара сил, момент якої дорівнює добутку плеча пари 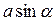на силу F:

.

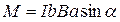Враховуючи, що добуток ab=S – площа, охоплена контуром і добуток IS=p_m, можемо переписати

.

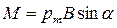3.2. Робота при переміщенні контуру з струмом в магнітному полі

Нехай є два провідника, до них під’єднано джерело струму і тоді по провідникам тече струм І.

Розташуємо на даних ще один провідник, який може вільно рухається по даних провідниках.

Припустимо, що паралельні гілки кола, яких ковзає провідник довжиною l. Якщо шину помістити в магнітне поле (вектор магнітної індукції перпендикулярні до площині), провідник почне рухатись. В процесі руху він переміщується паралельно самому собі, оскільки на нього діє сила

.

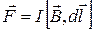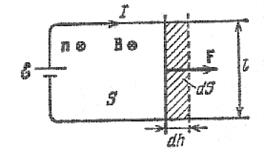Нехай провідник під дією цієї сили переміщується на відстань 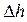. При цьому буде виконуватись механічна робота

.

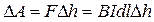Добуток 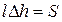– площа, яку охоплює провідник під час руху. Тоді

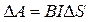. (3.4)

Рис. 3.2

Рівняння (3.4) виражає роботу по переміщенню провідника в магнітному полі.

Крім того робота може бути визначена через магнітний потік:

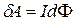. (3.5)

Для визначення знаку магнітного потоку, потрібно домовитись завжди брати нормаль до поверхні, охопленій контуром таким чином, щоб вона утворювала з напрямом сили струму правогвинтову систему. При цьому сила струму завжди повинна мати позитивний знак.

В нашому випадку магнітний потік і величина 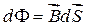є позитивними. Якби вектор магнітної індукції був направлений до нас або провідник переміщувався б в інший бік, то магнітний потік і приріст магнітного потоку були б негативними. В будь-якому з цих випадків рівність (3.4) можна записати у вигляді (3.5).

Отриманий результат справедливий для будь-якого напряму вектора В. Щоб переконатися в цьому, потрібно розкласти вектор магнітної індукції на три складові ():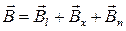

- _l – складова В, направлена вздовж провідника ( _l паралельна струму, тому не здійснює дії на провідник);

- _x – направлена вздовж переміщення, дана складова дає силу, перпендикулярну до переміщення і тому роботи вона не виконує;

- _n – складова, перпендикулярна до площини, в якій переміщується провідник і тому в формулі (4) потрібно брати саме B_n:

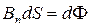. (3.6)

Маємо формулу (3.5), що і треба було довести.

Розглянемо будь-який контур при переміщенні в постійному однорідному магнітному полі (контур може довільним чином деформуватися). Розіб’ємо даний контур на нескінченно малі елементи струму і розглянемо їх нескінченно малі переміщення. В цих умовах магнітне поле, в якому переміщується кожен елемент струму можна вважати однорідним і для такого елементарного струму можна використати вираз:

,

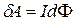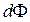– приріст потоку крізь контур від даного елементу контуру. Якщо додамо такі вирази для всіх елементів отримаємо формулу (3.6), де 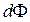– приріст магнітного потоку крізь весь контур..

Щоб знайти роботу сил Ампера при повному переміщенні контуру від початкового положення до кінцевого потрібно проінтегрувати (3.6).

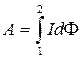. (3.7)

Якщо при даному переміщенні струм постійний, то

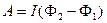, (3.8)

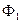та – магнітні потоки крізь контур в початковому і кінцевому положеннях.

Таким чином робота сил Ампера дорівнює добутку сили струму на приріст магнітного потоку крізь контур і рівняння (3.8) дає не лише величину, а й знак роботи, яка виконується.

Робота здійснюється не за рахунок енергії зовнішнього магнітного поля (магнітне поле не змінюється), а за рахунок джерела ЕРС, що підтримує струм в контурі.

Однією з характеристик магнітного поля є магнітний потік.

Розглянемо плоску пластинку, площею 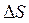, розміщену в однорідному магнітному полі індукцією В.

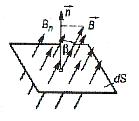Магнітним потоком через поверхню 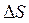називають фізичну величину, яка чисельно дорівнює добутку проекції вектора В на нормаль до поверхні на площу цієї поверхні.

,

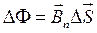або 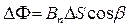, де α – кут між і .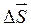

Рис. 3.3

Магнітний потік характеризує число ліній магнітної індукції, які проходять через дану поверхню. Залежно від того, який знак має 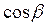магнітний потік може бути позитивним чи негативним. Знак 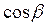залежить від вибору додатного напряму нормалі. Сам додатній напрям нормалі задається напрямом сили струму в контурі.

Магнітний потік через замкнену поверхню дорівнює нулю, оскільки число силових ліній, які входять в дану поверхню дорівнює числу силових ліній, які виходять з неї.

Змінити магнітний потік можна, якщо змінити магнітну індукцію (розмістити контур з постійною площею в неоднорідному магнітному полі), змінити орієнтацію контуру (обертаючи контур в однорідному полі).

В системі СІ одиниці вимірювання магнітного потоку – [Вб].

(1 Вб=1 Тл/1 м²).

3.3. Рух заряджених частинок в магнітному полі. Циклотрон

Нехай магнітне поле однорідне. Якщо частинка влітає в магнітне поле індукцією В, то залежно від знаку заряду, вона буде відхилятися праворуч, або ліворуч.

Радіус кривизни траєкторії R, по якій буде рухатись частинка можна знайти з умови рівності доцентрової сили і сили Лоренца.

,

.

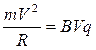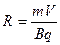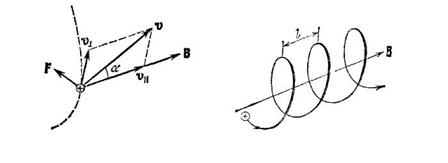
Якщо частинка, швидкість якої 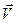буде направлена під певним кутом до ліній магнітної індукції, влітає в магнітне поле, то вона почне рухатися по гвинтовій лінії, причому швидкість розкладається на дві складові. Ще однією характеристикою руху частинки буде крок спіралі (визначається тангенціальною складовою швидкості). Радіус спіралі визначається нормальною складовою швидкості.

На елементарний заряд, що рухається одночасно в електричному та магнітному полях діє результуюча сила F:

.

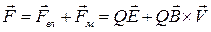Між електричною і магнітною складовими цієї сили є принципова відмінність: електричне поле змінює швидкість, а отже і кінетичну енергію частинки, однорідне магнітне поле змінює лише напрям її руху.

Якщо пропускати частинки через електричне і магнітне поля, що діють одночасно, то з рівняння для визначення радіусу спіралі R можна визначити їх питомі заряди (відношення заряду до маси). Швидкість частинки визначають з прискорюючої різниці потенціалів і тоді робота електричних сил чисельно дорівнює кінетичній енергії частинки.

, .

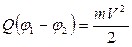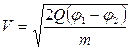Рис. 3.4

Радіус траєкторії визначається експериментально. За відомим значенням В і 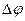визначають питомий заряд частинки.

.

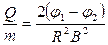Прилади, за допомогою яких можна поділити заряджені частинки за їх питомими зарядами називають масс-спектрографами.

Структури атомних ядер, бомбардуючи їх частинками, які мають велику енергію або швидкість досліджують за допомогою циклотронів (прискорювачів заряджених частинок).

В циклотроні заряджені частинки рухаються між плюсами електромагніту, велику кількість раз проходять через магнітне поле. При цьому енергія частинки щоразу зростає на 10² – 10³ еВ. Рухом частинок керують за допомогою поперечного магнітного поля. На заряджену частинку в магнітному полі діє сила Лоренца, внаслідок чого частинка рухається по колу сталого радіуса R. Якщо її маса і швидкість не змінюються, то сила Лоренца дорівнює силі, спричиненій доцентровим прискоренням.