
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модификация метода ускоренной ориентации динамических символов объектов на основании применения алгоритма Брезенхема.
|
|
Исследование применений предлагаемого метода показало, что количество операций существенно сокращается в случае, если дополнительно к нему применить алгоритм Брезенхема для построения прямых.
Этот алгоритм основан на следующем факте: прямая 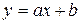 на экране отображается в виде «ступенек» – т.е. в зависимости от знака числа
на экране отображается в виде «ступенек» – т.е. в зависимости от знака числа 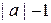 либо каждая строка, либо каждый столбец точек экрана состоят из отрезков, имеющих цвет прямой, причем длина этих отрезков отличается не более чем на единицу. Тогда для прорисовки этой прямой достаточно вычислить длины этих отрезков
либо каждая строка, либо каждый столбец точек экрана состоят из отрезков, имеющих цвет прямой, причем длина этих отрезков отличается не более чем на единицу. Тогда для прорисовки этой прямой достаточно вычислить длины этих отрезков 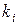 с помощью одной операции деления с плавающей точкой, а затем либо по каждой строке
с помощью одной операции деления с плавающей точкой, а затем либо по каждой строке 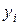 , либо по каждому столбцу
, либо по каждому столбцу 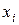 осуществить цикл закрашивания точек с координатами
осуществить цикл закрашивания точек с координатами 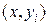 ..
.. 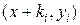 , либо
, либо 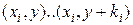 , т.е. на каждом шаге производится сложение по строкам (столбцам) и еще по одной операции сложения для каждого закрашиваемого пикселя. В результате прорисовка отрезков на экране значительно убыстряется.
, т.е. на каждом шаге производится сложение по строкам (столбцам) и еще по одной операции сложения для каждого закрашиваемого пикселя. В результате прорисовка отрезков на экране значительно убыстряется.
Предлагается подсчитать значения тангенса и котангенса угла поворота 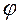 и присвоить dx1: =h1∙ tg(
и присвоить dx1: =h1∙ tg( 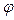 ); dy1: =h2∙ ctg(
); dy1: =h2∙ ctg( 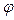 ). Матрица растрового изображения символа
). Матрица растрового изображения символа 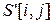 , которая соответствует символу после поворота на угол
, которая соответствует символу после поворота на угол 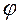 , вычисляется по циклу:
, вычисляется по циклу:
x1: =x’-dx2; y1: =y’-dy2;
От i: =0 до X начать
j: =0; x: =x+dx1; y1: =y1+1;
если int{x}=int{x-dx1} то x1: =x1+1;
x2: =x1; y2: =y1;
S[i, j]: =S[x1, y1];
От j: =1 до Y начать
x2: =x2+1; y: =y+dy1;
если int{y2}=int{y2-dy1} то y2: =y2+1;
S’[x2, y2]: =S[i, j];
конец цикла; конец цикла;
Очевидно, что метод быстрого поворота с применением алгоритма Брезенхема позволяет выполнять меньшее количество операций за счет того, что здесь совершается лишь одно сложение вещественных чисел, а две другие операции сложения в теле цикла осуществляются для целых чисел.
Первоначальное растровое изображение объекта можно представить в виде объединения некоторого количества отрезков, параллельных оси абсцисс. Следовательно, для поворота изображения необходимо осуществить поворот всех этих отрезков на один и тот же угол 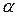 . Таким образом, осуществляется отображение серии отрезков заданной длины с коэффициентом наклона
. Таким образом, осуществляется отображение серии отрезков заданной длины с коэффициентом наклона 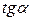 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Рассмотрим предлагаемую модификацию подробнее. Для данного 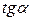 , если он меньше единицы, определяется его целая и дробная часть соответственно
, если он меньше единицы, определяется его целая и дробная часть соответственно 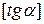 и
и 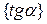 . Тогда присвоим
. Тогда присвоим 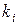 значение
значение 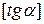 . Затем определяются значения
. Затем определяются значения 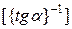 и
и 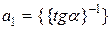 соответственно, а тем
соответственно, а тем 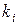 , где
, где 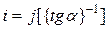 (
(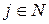 ) присваиваются значения
) присваиваются значения 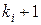 . После этого определяются значения
. После этого определяются значения 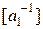 и
и  , соответственно и тем
, соответственно и тем 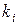 , где
, где 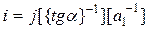 (
(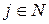 ) присваиваются значения
) присваиваются значения 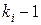 . Далее, аналогично, определяются значения
. Далее, аналогично, определяются значения 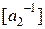 и
и 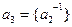 соответственно и тем
соответственно и тем 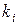 , где
, где 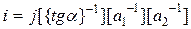 (
(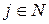 ) присваиваются значения
) присваиваются значения 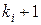 . Такой процесс продолжается до тех пор, пока число
. Такой процесс продолжается до тех пор, пока число 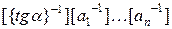 не станет больше количества пикселей по вертикальной оси окна экрана или же максимальной высоте изображения символа, подвергающегося повороту.
не станет больше количества пикселей по вертикальной оси окна экрана или же максимальной высоте изображения символа, подвергающегося повороту.
Аналогично в случае, если 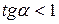 , те же операции производятся для начального числа
, те же операции производятся для начального числа 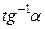 и цикл осуществляется до тех пор, пока
и цикл осуществляется до тех пор, пока 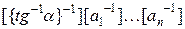 не станет больше количества пикселей по горизонтальной оси экрана или же максимальной ширине поворачиваемого изображения.
не станет больше количества пикселей по горизонтальной оси экрана или же максимальной ширине поворачиваемого изображения.
Таким способом можно получить значения длин отрезков 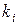 , представляющих отображаемую прямую. Следовательно, можно осуществить алгоритм построения отрезка закрашиванием точек с координатами
, представляющих отображаемую прямую. Следовательно, можно осуществить алгоритм построения отрезка закрашиванием точек с координатами 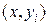 ..
.. 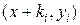 (либо
(либо 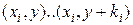 ), т.е. на каждом шаге осуществляется сложение по строкам (столбцам) и еще по одной операции сложения для каждого закрашиваемого пикселя.
), т.е. на каждом шаге осуществляется сложение по строкам (столбцам) и еще по одной операции сложения для каждого закрашиваемого пикселя.
Отметим, что значения 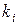 можно получить заранее и хранить их в памяти процессора так же, как и значения тригонометрических функций от углов, поскольку количество возможных комбинаций
можно получить заранее и хранить их в памяти процессора так же, как и значения тригонометрических функций от углов, поскольку количество возможных комбинаций 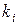 , очевидно, ограничено, т.к. количество элементов массива
, очевидно, ограничено, т.к. количество элементов массива 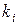 не может превышать количества пикселей в строке или столбце окна экрана, а также максимальной ширины и высоты поворачиваемого изображения, и ту же величину не может превышать максимальный элемент
не может превышать количества пикселей в строке или столбце окна экрана, а также максимальной ширины и высоты поворачиваемого изображения, и ту же величину не может превышать максимальный элемент 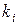 .
.
Способ нахождения 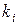 можно ускорить, если на каждом шаге брать не целую и дробную часть, а округленное целое, и, соответственно, разность между округленным и самим числом.
можно ускорить, если на каждом шаге брать не целую и дробную часть, а округленное целое, и, соответственно, разность между округленным и самим числом.
Таким образом, предлагаемый метод ускоренного экономичного поворота динамических символов обеспечивает меньшее количество операций за счет того, что при его использовании совершается лишь одна операция сложения вещественных чисел и две операции сложения целых чисел. Операции сложения для целых значений производятся в а=4 раза быстрее, чем те же операции над действительными числами особенно, если учесть, что в нашем случае вещественные числа представлены 16-тью разрядами.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
С учетом изложенного количество операций при выполнении поворота будет равно 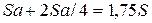 , где
, где 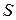 - количество элементов в матрице символа, в то время как известные методы поворота предусматривают не менее
- количество элементов в матрице символа, в то время как известные методы поворота предусматривают не менее 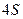 операций, то есть время выполнения поворота составит 22% от времени выполнения описанных в литературе алгоритмов.
операций, то есть время выполнения поворота составит 22% от времени выполнения описанных в литературе алгоритмов.
|
|
