💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Матричный метод

Движение объекта отображается на экране как перемещение видеосимвола S, представленного некоторым подмножеством множества точек квадратной n x n матрицы пикселей. В равноотстоящие дискретные моменты времени t_k (k = 1, 2,...) на вход программы управления движением символа поступают координаты точки Р ₂ (х ₂, у ₂), в которую символ S должен быть перемещен из предыдущей точки Р ₁ (х ₁, у ₁). Задача состоит в том, что необходимо переместить символ S из точки Р ₁ в точку Р ₂ и повернуть продольную ось символа на новое направление движения вдоль вектора с минимально возможным использованием вычислительных ресурсов. При этом движение должно происходить без деформации символа S (требование константности формы).

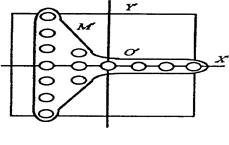
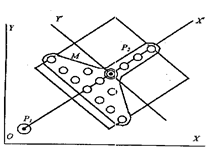
Введем две системы координат: основную ОХY, ось ОХ которой свяжем с нижней, а ось ОY - с левой границами экрана и О ' Х ' Y ' – систему для задания новых координат точек символа, изменившего ориентацию своего движения на определенный угол (рис.4.1.2, а и рис.4.1.2, б).

Обе координатные системы - декартовы прямоугольные с одинаковыми масштабами по всем четырем осям. Расположим квадратную n x n матрицу-носитель символа так, что точка пересечения ее диагоналей находится в центре О ' дополнительной системы координат О ' Х ' Y '. Тогда положение и конфигурация символа определяются заранее заданными координатами некоторых точек матрицы в системе X ' O ' Y '. Конфигурацию символа предполагаем симметричной относительно его продольной оси, а центром изображения S считаем точку О'. Обозначим точками Р ₁(х ₁, у ₁) и Р ₂(х ₂, у ₂) предыдущее и последующее положения центра символа. Символ считаем расположенным в точке Р_i (х_i, у_i), если его центр О ' находится в точке Р_i (х_i, у_i).

Перенести символ S в точку Р ₂(х ₂, у ₂) означает воспроизвести его в этой точке так, чтобы центр О ' имел координаты (х ₂, у ₂), а продольная ось символа совпала с направлением вектора . Такое движение достигается параллельным переносом системы координат Х'О'Y' в точку Р ₂(х ₂, у ₂):

и поворотом ее на угол φ:

- угол наклона прямой к горизонтали.

a)

б)

Рис. 4.1.2. Графическое отображение матрицы и символа

в координатах ОХУ и О'Х'У'.

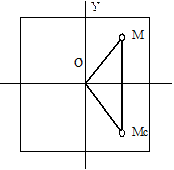
Рис.4.1.2. Графическое отображение симметричных точек символа в координатах (X'O'Y').

Одновременный перенос и поворот описывается преобразованием:

В (2.4) х ₂, у ₂ — координаты нового начала, х, у — координаты точки М (образа), х ', у ' — координаты точки М' (прообраза точки М). Координаты (х ', у ') являются постоянными и задаются при исходном положении символа.

Чтобы найти новые координаты одной точки символа надо выполнить 8 арифметических операций (4.1.4) и 3 операции (4.1.3) – 11 операций (предполагаем, что тригонометрические функции sin φ, cos φ, arctg φ не вычисляются, а считываются из таблиц).

Для размера матрицы n x n, равному 10 х 10, т.е. 100-точечного символа это потребует 1100 операций. При быстродействии видеоконтроллера 40 МГц на воспроизведение такого символа на очередном шаге будет затрачено около 3 миллисекунд: 2, 5 х 10^-6 х 1, 1 х 10³ = 3 мс, что недопустимо в подавляющем числе применений. Это объясняется тем, что размер матрицы достигает, как правило, больших размеров, поворот осуществляется пошагово, чтобы обеспечить плавность, последовательно на несколько углов, составляющих этот поворот, а количество символов может составлять десяток и более.

Очевидно, что затраты памяти на хранение одного символа существенно сокращаются тогда, когда он определен только точками, задающими его конфигурацию. Причем число матриц с «записанными» его конфигурациями должно быть столько, сколько предусмотрено угловых шагов при отображении его вращения. При этом, в соответствии с курсом, надо успевать рассчитывать, согласно (4.1.1) на каждом шаге новые координаты центра матрицы.