Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Понятие аффинных преобразований.

Одной из главных особенностей функционирования ГИС РВ является организация динамики символов объектов, включающая такие операции как: параллельный перенос, поворот и изменение масштаба, при реализации которых часто допустимы аффинные преобразования:

1. Перенос, задаваемый простейшими соотношениями:

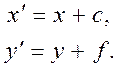
(1.2.1)

2. Поворот вокруг начальной точки на угол 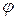, описываемый формулой:

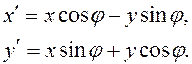
(1.2.2)

3.Растяжение (сжатие) вдоль координатных осей, задаваемое в виде:

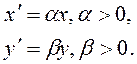
(1.2.3)

Осуществляя композицию описанных выше процедур (1.2.1-1.2.3), аффинное преобразование трансформируется в преобразование подобия, содержащее преобразования сдвига, поворота и изменения масштаба:

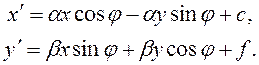
(1.2.4)

Отсюда вытекает, что движение символов на экране ГИС ОУ можно задать с помощью последовательности операций поворота и параллельного переноса. Операция параллельного переноса является простой для программной реализации и достаточно быстрой, поскольку требует не более двух операций сложения целых чисел для каждой точки символа (1.2.4). Операция поворота символа требует значительного количества машинных ресурсов, поскольку для ее выполнения в общем случае осуществляется четыре операции умножения и две операции сложения действительных чисел (1.2.4).