Метод ускоренной ориентации динамических символов объектов, отображаемых на экране ГИС РВ, и его модификация на основании применения алгоритма Брезенхема.

При наличии большого числа различных символов, двигающихся, как правило, с различными скоростями, эти операции требуется производить как можно быстрее (чтобы построить кадр не более чем за 20 мсек − это время, необходимое для соблюдения режима реального времени, т.е. обеспечить скорость формирования кадра равную 50 кадр./сек.), что дает возможность освободить процессор системы для решения других задач, например, анализа динамической обстановки, расчетов, связанных с вычислением подлетного времени и др. Для этого, нами предлагается метод быстрого поворота символа, заданного прямоугольной матрицей размером 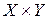точек, суть которого состоит в следующем.

Назовем абсолютной системой координат координатную сетку, единичные клетки которой совпадают с пикселями экрана. А относительной системой координат назовем координатную сетку, единичные клетки которой совпадают с элементами матрицы символа .

Выберем точку начала относительной системы координат 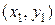. Для удобства вычислений можно взять одну из вершин прямоугольной матрицы, в которой хранится растровое изображение символа – . Для этой точки вычисляются ее координаты 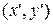после поворота с помощью синусно-косинусного преобразования:

x': =x₁+(x₀-x₁)∙ cos(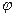)+(y₁-y₀)∙ sin();

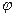y': =y₁+(y₀-y₁)∙ cos(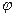)+(x₀-x₁) sin().

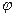Здесь: 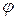– угол поворота; x₀, y₀ – координаты точки, относительно которой совершается поворот.

Затем вычисляются проекции границ единичной клетки относительной системы координат на абсолютную:

dx1: =h1∙ sin();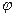

dy1: =h1∙ cos();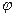

dx2: = h2∙ cos();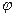

dy2: =- h2∙ sin(),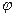

где h1, h2 – длины сторон единицы экрана.

Далее от полученных значений x' и y' новые значения рассчитываются с помощью цикла по клеткам относительной системы координат (также определяется новый цвет точек при повороте):

x1: =x’-dx2; y1: =y’-dy2;

От i: =0 до n начать

j: =0; x1: =x1+dx2; y1: =y1+dy2;

x2: =x1; y2: =y1;

S[i, j]: =S[x1, y1];

От j: =1 до m начать

x2: =x2+dx1; y2: =y2+dy2;

S’[x2, y2]: =S[i, j];

конец цикла;

конец цикла;

Предложенный метод позволяет получить из матрицы символа размерности 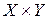матрицу 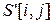большей размерности: 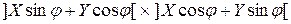, здесь 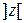- наименьшее целое число, большее 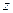, в которой 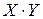пикселей закрашены в определенные цвета. Это значит, что матрица 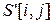содержит неинициализированные элементы. Для избежания такой ситуации предлагается метод обратного преобразования, в соответствии с которым нужно повернуть изображение 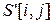на угол - .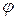