Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Решение задачи методом отсекающих плоскостей (метод Гомори). Приведём решение исходной задачи симплекс-методом, опустив требование целочисленности

Приведём решение исходной задачи симплекс-методом, опустив требование целочисленности. Оно представлено в таблице 2.53.

Таблица 2.53

Значение переменной x₄ не удовлетворяет требованиям целочисленности. Поэтому вводим дополнительное отсечение, исходя из данной строки.

Ограничения для частично-целочисленных задач по методу Гомори формируются в виде:

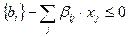
где 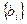- дробная часть свободного члена базисной переменной,

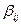- коэффициент, рассчитываемый для небазисных переменных.

Для 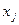не подчиненных требованию целочисленности коэффициент 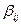рассчитывается по формуле:

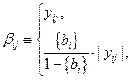
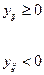
Для 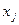подчиненных требованию целочисленности коэффициент 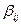рассчитывается по формуле:

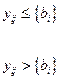
Вычислим отсекающую плоскость и представим ее в форме Таккера:

X9=-1/2-(-3/4*X3-1/2*X5-1/2*X7-3/4*X8)

Добавим в базис таблицы 2.53 полученное ограничение. Результат представлен в таблице 2.54.

Таблица 2.54

Используем двойственный симплекс-метод. Вводим в базис X8, выводим из базиса X9.

Таблица 2.55

Полученное оптимальное решение удовлетворяет требованию целочисленности х₄.

Ответ: Y=-55/4, X=(59/12; 5/12; 0; 4; 0; 131/4; 0; 2/3; 0).