Студопедия

Главная страница Случайная страница

Разделы сайта

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника






  • Как продвинуть сайт на первые места?
    Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.
    Ускорение продвижения
    Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.
    Начать продвижение сайта

    • Решение задачи методом отсекающих плоскостей (метод Гомори)


    ⇐ ПредыдущаяСтр 3 из 14Следующая ⇒




    Для решения целочисленной задачи воспользуется решением линейной задачи без требования целочисленности. Перепишем симплекс-таблицу решённой задачи из пункта 1.3.

    Таблица 2.1

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8
    X5         -5     -2  
    X1 9/2       -1   -1/2    
    X2 7/4       -2   1/4 -1 1/2
    X3 5/4       -1   -1/4   1/2
    Y -16                

     

    На основе этой симплекс-таблицы для базисной переменной x1 (у нее наибольшая дробная часть) строим уравнение отсекающей плоскости по следующей формуле:

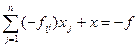
    где f – дробная часть свободного члена;

    fij – дробные части коэффициентов строки.

    Представим новое ограничение в форме Куна-Таккера:

    x9=-1/2-(-5/16*x3-7/8*x5-5/8*x7-13/16*x8)

    Добавляем это ограничение к условиям оптимального решения и решаем новую расширенную задачу симплекс-методом.

    Таблица 2.2

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X4 7/2     -3/4   1/2   1/2 -3/4  
    X6 229/8     21/16   23/8   29/8 -99/16  
    X2 5/8     13/16   -1/8   -3/8 5/16  
    X1 35/8     11/16   1/8   3/8 -13/16  
    X9 -5/8     -5/16   -7/8   -5/8 -13/16  
    Y -109/8     139/16   9/8   11/8 3/16  

    Используем двойственный симплекс-метод. Вводим в базис X8, выводим из базиса X9.

    Таблица 2.3

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X4 53/13     -6/13   17/13   14/13   -12/13
    X6 434/13     48/13   124/13   109/13   -99/13
    X2 5/13     9/13   -6/13   -8/13   5/13
    X1                   -1
    X8 10/13     5/13   14/13   10/13   -16/13
    Y -179/13     112/13   12/13   16/13   3/13

    Решение оптимально. Так как переменная X8, подчиненная требованию целочисленности, и имеет дробное значение, то необходимо ввести дополнительное сечение относительно этой переменной:

    x10=-10/13-(-5/13*x3-1/13*x5-10/13*x7-10/13*x9)

     

    Таблица 2.4

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X4 53/13     -6/13   17/13   14/13   -12/13  
    X6 434/13     48/13   124/13   109/13   -99/13  
    X2 5/13     9/13   -6/13   -8/13   5/13  
    X1                   -1  
    X8 10/13     5/13   14/13   10/13   -16/13  
    X10 -10/13     -5/13   -1/13   -10/13   -10/13  
    Y -179/13     112/13   12/13   16/13   3/13  

    Используем двойственный симплекс-метод. Вводим в базис X9, выводим из базиса X10.

    Таблица 2.5

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X4           7/5         -6/5
    X6       15/2   103/10         -99/10
    X2       1/2   -1/2   -1     1/2
    X1       3/2   11/10         -13/10
    X8           6/5         -8/5
    X9       1/2   1/10         -13/10
    Y -182/13     17/2   9/10         3/10

    Полученное решение удовлетворяет поставленным ограничениям и требованиям целочисленности. Решение является оптимальным.

    Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
    Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
    Что умеет делать SeoHammer
    — Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
    — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
    — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
    — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
    SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.
    Зарегистрироваться и Начать продвижение

     

    Ответ: Y=-14, X=(6; 0; 0; 5; 0; 41; 0; 2; 1; 0).

     



    ⇐ Предыдущая12345678910Следующая ⇒




    © 2023 :: MyLektsii.ru :: Мои Лекции
    Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
    Копирование текстов разрешено только с указанием индексируемой ссылки на источник.