Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Дискретное преобразование Лапласа

Дискретное преобразование Лапласа является функциональным преобразованием решетчатых функций.

Как известно, непрерывная функция времени имеет изображение по Лапласу:

.

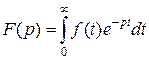Если в эту формулу подставить текущее время в виде 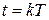, где k = 1, 2,..., то интеграл можно заменить суммой

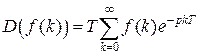(2.1)

или в относительных единицах при q = рТ

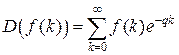. (2.2)

Для смещенных функций

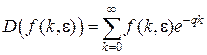. (2.3)

Дискретное преобразование Лапласа имеет смысл только в том случае, если ряд, стоящий в правой части уравнений (2.2), (2.3) сходится.

Параметр преобразования q в общем случае – комплексное число .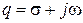

Чем больше значение σ, тем быстрее сходится ряд (2.2).

Абсциссой сходимости называется такое значение 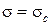, для которого при ряд сходится, а при 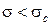расходится.

Изображение решетчатой функции в комплексной плоскости есть периодическая вдоль мнимой оси функция

.

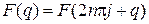Поэтому функция F (q) полностью определена в полосе, соответствующей .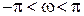

Обратное преобразование Лапласа производится по формуле

,

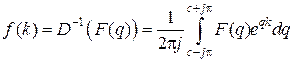где 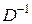– символ обратного дискретного преобразования Лапласа,

с – произвольная постоянная, удовлетворяющая условию .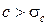

Для смещенной решетчатой функции

.
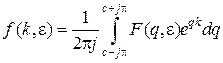