Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Решетчатые функции. Разностные уравнения

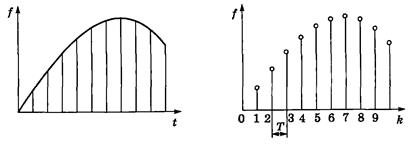
На рис. 2.5 представлены непрерывная функция времени f (t) и соответствующая ей решетчатая функция , значения которой определены для t_k = kT. Таким образом, вместо непрерывного аргумента t мы имеем целочисленный аргумент k (номер интервала времени).

а) б)

Рис. 2.5. Непрерывная (а) и решетчатая (б) функции

Решетчатой функцией называется действительная функция целочисленного аргумента.

Для решетчатых функций вводятся разности различных порядков, которые аналогичны производным для непрерывных функций.

Разность первого порядка

.

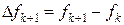Разность второго порядка

.

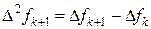Разность i -гo порядка выражается рекуррентным [1] соотношением

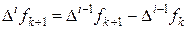
или, с учетом выражений разностей,

,

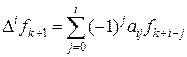где 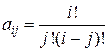- биномиальные коэффициенты.

Уравнение, содержащее решетчатую функцию и ее разности различных порядков, называется уравнением в конечных разностях или разностным уравнением (аналог дифференциального уравнения). Линейное разностное уравнение имеет вид

.

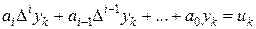Заменяя разности их выражениями, получим разностное уравнение в рекуррентной форме

.

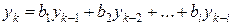Наиболее часто применяются системы разностных уравнений первого порядка в рекуррентной форме. Они могут быть получены в результате применения к системам дифференциальных уравнений первого порядка численных методов.

Разностные уравнения по существу являются рекуррентными соотношениями, позволяющими при i = 0, 1, 2,... последовательно шаг за шагом (т.е. рекуррентно) вычислять значения выходной величины 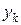при заданных ее начальных значениях и любых заданных аналитически, графически или таблично значениях входной величины .

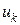Решение разностного уравнения 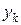дает значения выходной величины лишь в дискретные моменты времени t = kT. Во многих случаях этого вполне достаточно для суждения о поведении системы. Если же возникает необходимость в получении информации об изменении выходной величины в любой момент времени, то используется смещенная последовательность

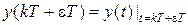
или в сокращенной записи 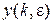, где ε – параметр, которому можно придавать любые значения в пределах 0 ≤ ε ≤ 1. Если ε изменять непрерывно в указанных пределах, то 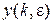совпадает с y (t).