Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Устойчивость импульсных САР

Импульсная САР в замкнутом состоянии устойчива в том случае, если все полюсы ее передаточной функции (ПФ) имеют отрицательные вещественные части или, что то же самое, если они лежат в левой части полосы 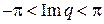комплексной плоскости.

Об устойчивости разомкнутой импульсной системы можно судить по полюсам ПФ, ее приведенной непрерывной части. Если приведенная непрерывная часть устойчива, то разомкнутая система будет устойчивой.

Так как частотные характеристики импульсной системы аналогичны АФХ непрерывных систем, то и здесь для исследования устойчивости используется критерий Найквиста. Согласно критерию Найквиста, замкнутая импульсная система устойчива, если частотная характеристика 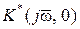устойчивой разомкнутой системы не охватывает точку (–1; j 0) при изменении 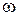от 0 до .

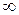Чтобы замкнутая импульсная система была устойчивой при неустойчивой приведенной непрерывной части, необходимо, чтобы разность между числом положительных и отрицательных переходов частотной характеристики 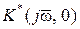отрезка действительной оси (– ∞, +1) была равна s/2, где s – число полюсов с положительной действительной частью ПФ разомкнутой САР.

На рис. 2.6 изображена частотная характеристика разомкнутой импульсной системы 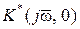. Там же нанесена точка (-1, j 0), лежащая вне частотной характеристики, и проведена штриховая окружность для определения запаса устойчивости по фазе 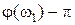. Величина h характеризует запас устойчивости по модулю.

Рис. 2.6. Частотная характеристика разомкнутой импульсной системы

Другой метод исследования основан на выделении областей устойчивости в плоскости комплексной величины z путем отображения линейной оси плоскости р (рис. 2.7, а) на плоскость z.

Для этой цели необходимо сделать подстановку 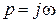в z-преобразование и менять затем частоту 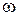в пределах от до .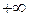

Таким образом, получаем 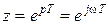. При изменении частоты в этих пределах в плоскости z (рис. 2.7, б) получаем окружность единичного радиуса, ограничивающую область устойчивости.

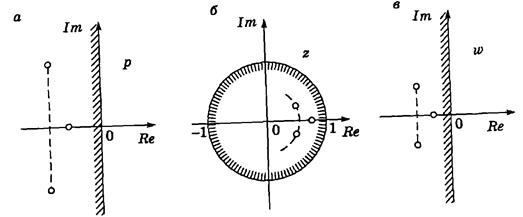
Рис. 2.7. Области устойчивости на плоскостях переменных р, z, и w

Условием устойчивости будет нахождение особых точек (полюсов) ПФ замкнутой системы Ф(z) внутри этой окружности. Следовательно, корни характеристического уравнения 1 + K (z) = 0 должны быть ограничены по модулю | z | < 1.

Для характеристического уравнения первого порядка очевидное условие устойчивости

.

Для уравнения второго порядка

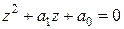(2.8)

путем вычисления его корней получаются три условия устойчивости:

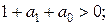
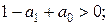(2.9)

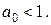
Для уравнения третьего порядка

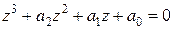
условия устойчивости:

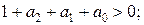
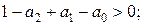
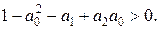
Для уравнений более высокого порядка целесообразно применить w -преобразование, с помощью которого окружность единичного радиуса отображается на мнимую ось плоскости комплексной величины w. Для преобразования используется подстановка

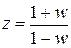(2.10)

или

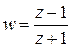. (2.10)

При подстановке 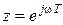будем иметь

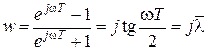, (2.11)

где 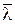представляет относительную псевдочастоту. При малых частотах 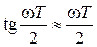и абсолютная псевдочастота .

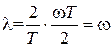При изменении частоты 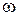в пределах от 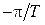до 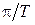псевдочастота изменяется от до 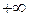, а комплексная величина w движется по мнимой оси от 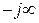до 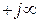. Областью устойчивости в этом случае оказывается вся левая полуплоскость (рис. 2.7, в).

Поэтому для ПФ с w -преобразованием могут использоваться те же критерии устойчивости, что и для непрерывных систем.

Использование w -преобразования дает возможность построить в функции псевдочастоты 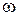JIAX и ЛФХ для импульсных систем, аналогичные логарифмическим характеристикам непрерывных систем.