
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение преобразователя двоичного кода в код Грея
|
|
Преобразование А(х) = (an,..., aр,..., a1), где a = xp Å xp, если р = 1, 2,..., n-1, и aр = xn, если р = n, определяет алгоритм построения кода Грея.
Код Грея используют в преобразованиях аналоговых физических сигналов в цифровые сигналы с погрешностью, не превышающей значение младшего разряда двоичного числа X.
Важно: код Грея относится к таким, в которых при переходе от любой кодовой комбинации к следующей изменяется только один разраяд. Код Грея можно получить по соотношению 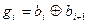 , где
, где 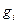 - значение разряда кода грея,
- значение разряда кода грея, 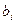 - значение разряда двоичного кода, преобразуемого в код грея. Ряд левее старшего для двоичного кода считается нулевым.
- значение разряда двоичного кода, преобразуемого в код грея. Ряд левее старшего для двоичного кода считается нулевым.
Пример: Записать число 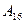 в коде Грея. Перепишем это число в двоичном коде: 1010, тогда преобразование будет выглядеть следующим образом:
в коде Грея. Перепишем это число в двоичном коде: 1010, тогда преобразование будет выглядеть следующим образом:
| Х | ||||
| * | ||||
| Х |
(*-всегда ноль). Сложив столбцы в таблице по модулю 2 и отбросив последний (где есть «Х»), получили число 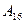 или двоичное 1010 в коде Грея. Оно имет значение 1111. Это можно увидеть и на временных диаграммах (рис. 6.38)
или двоичное 1010 в коде Грея. Оно имет значение 1111. Это можно увидеть и на временных диаграммах (рис. 6.38)
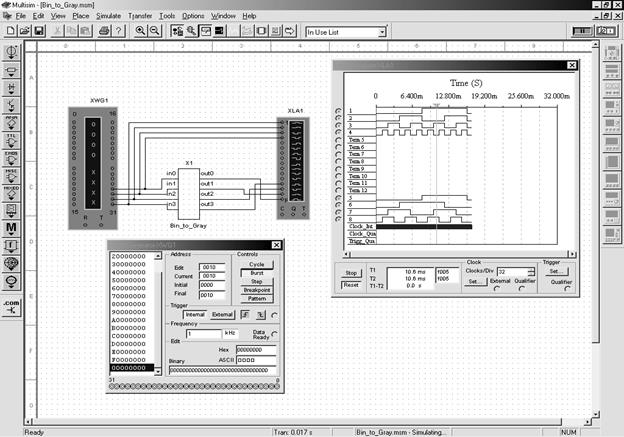
Рис. 6.38 Работа преобразователя двоичного кода в код Грея
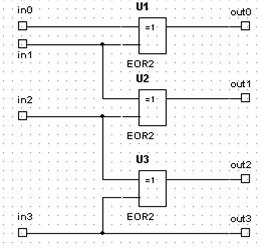
Рис. 6.39 Структура преобразователя двоичного кода в код Грея (блок Bin_to_Gray)
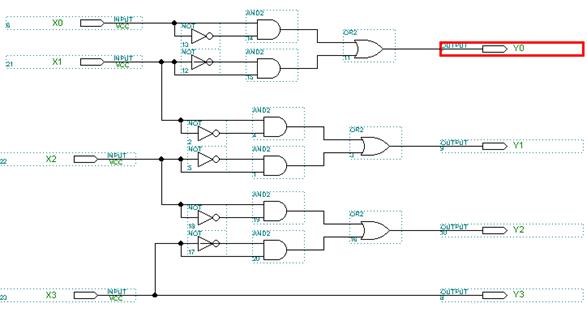
Рис. 6.40 Преобразователь двоичного кода в код Грея в пакете
MAX+Plus II
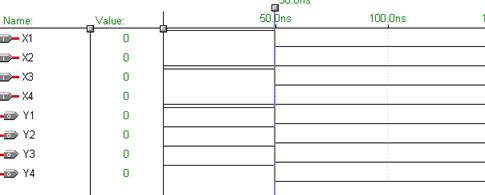
Рис. 6.41 Временные диаграммы
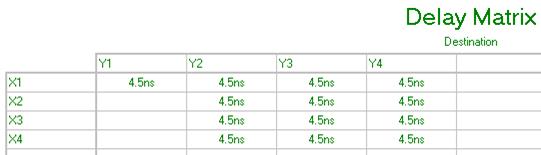
Рис. 6.42 Матрица временных задержек
Программа:
CONSTANT t=3
SUBDESIGN preobraz_dvoich_v_kod_greay
(X[3..0]: INPUT;
Y[3..0]: OUTPUT;
)
VARIABLE q[3..0]: NODE;
BEGIN
FOR i IN 0 TO t GENERATE
X[i+1] = q[i];
END GENERATE;
q[3] = GND;
Y[3..0] = X[3..0] $ q [3..0];
END;
Преобразование кода Грея в двоичный код описывается выражением xp = ap Å xp+1, если р = 1, 2,..., n-1, и x = an, если р = n. Схема преобразователя А(х) для четырехразрядных двоичных чисел Х = (x4, х3, x2, x1) показано на рис. 6.43.
Пример: Получить из числа 1011, записанного в коде Грея, его двоичное значение.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Тут нужно пояснить. Бинарное число в старшем разряде всегда будет иметь то значение, которое было в старшем разряде кода Грея. Остальные значения получаются после сложения по модулю 2 соответствующих разрядов (если записаны как в таблице, тогда по диагонали).
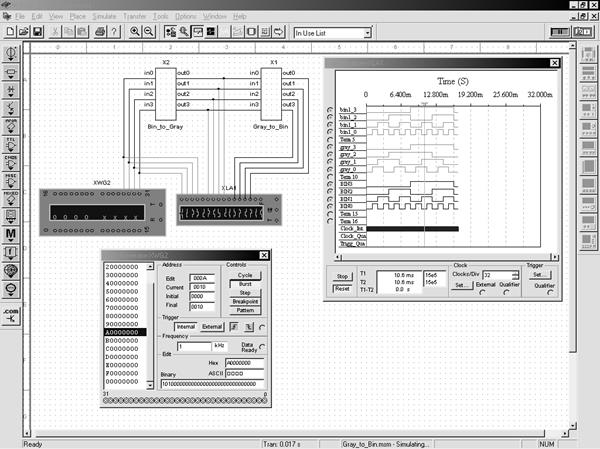
Рис. 6.43 Работа преобразователя кода Грея в двоичный код (*)
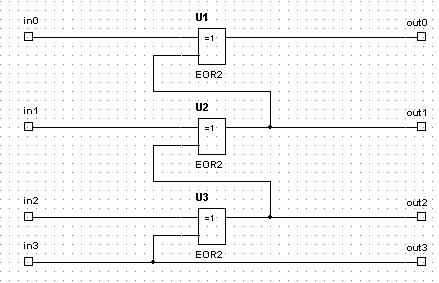
Рис. 6.44 Внутренняя структура элемента Gray_to_Bin
(преобразователя кода Грея в двоичный код)
(*) Примечание. Для получения кода Грея, из которого нужно получить двоичный код, можно воспользоваться рассмотренным в предыдущем примере преобразователем двоичного кода в код Грея (модуль Bin_to_Gray).
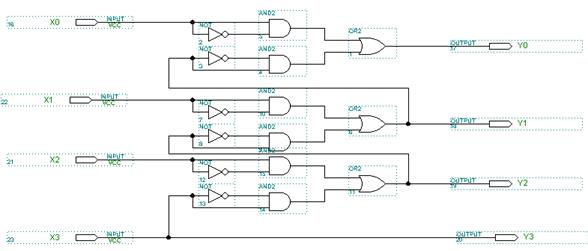
Рис. 6.44 Преобразователь кода Грея в двоичный код в
пакете MAX+Plus II
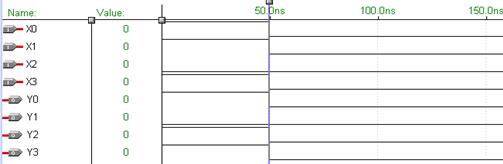
Рис. 6.45 Временные диаграммы
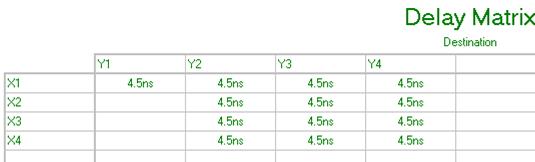
Рис. 6.46 Матрица временных задержек
Программа:
CONSTANT t=3;
SUBDESIGN
(X[3..0]: INPUT;
Y[3..0]: OUTPUT;
)
BEGIN
Y[3] = X[3];
FOR i IN 0 TO t GENERATE
y[t-1] = X[t-1] $ Y[t+1-i];
END GENERATE;
END;
|
|
