Преобразователь обратного кода в прямой

Если на вход схемы преобразователя четырехразрядного прямого кода в обратный код (см. рис. 6.20) подать дополнительный код, то на выходе получим прямой код.

6.4.6 Построение преобразователя двоичного кода в двоично-десятичный

Десятичные сумматоры применяются в тех случаях, когда числа X и Y представлены в десятичной системе счисления двоично-десятичным кодом 8-4-2-1 и требуется представлять сумму S в этом же коде. Числа X и Y записываются в виде:

Х’=х_n,...х₁х₀ Y’=y_n,... у₁, у₀

Код 8 - 4 - 2 - 1 неудобен для выполнения арифметических операций, в частности из-за сложности обнару­жения переноса в следующую тетроду при Х_р + Y_р > 10. При вычитании десятичных чисел X' и Y’ дело обстоит еще сложнее – требуется вводить преобразователь кода 8 - 4 - 2 - 1 отрицательных чисел в допол­нение до 9 (или до 10).

Десятичные сумматоры для сложения и вычитания чисел Х и Y можно построить на двоичных суммато­рах, если использовать код с избытком 3. Код 8 - 4 - 2 - 1 для числа Х_р + 3 называется кодом с избытком 3 числа Х_ри обозначается через {А_р}. Для сложения 4-разрядных двоичных кодов {Х_р} и {Y_р} можно использовать 4-разрядные двоичные сумматоры.

Рассмотрим особенности сложения положительных чисел А_р и Y_р в коде с избытком 3. Если Х_р + Y_р > 10, то {Х_р} + {Y_р} = Х_р + 3 + Y_р + 3 > 16, и на выходе двоичного сумматора возникает перенос С_p+1= 1 в следующий десятичный разряд, а остаток суммы будет равен {Х_р} + {У_р} - 16, в то время как он должен быть равен

{X_p+Y_p-10}=X_p+Y_p-10+3={X_p}+{Y_p}-16+3.

Поэтому к остатку суммы {X_p}+{Y_p}-16 следует прибавлять число 3.

Если Х_р + Y_р < 10, то {X_p}+{Y_p}< 16 и на выходе двоичного сумматора перенос отсутствует (C_p+1 = 0), а сумма {Х_р} + {Y_р} = {Х_р + Y_р} + 3. Поэтому из суммы {Х_р} + {Y_р} следует вычесть число 3, чтобы получить величину {Х_р + Y_р}, которая является кодом с избытком 3 суммы Х_р+Y_р. Вычитание какого-либо числа эквивалентно сложению его с дополнением до 2ⁿ, поэтому вместо вычитания числа 3 можно прибавить число 2⁴ – 3 = 13 = 1101.

Таким образом, если перенос возникает, то к остатку суммы следует прибавить число 3, а если он от­сутствует, то к сумме следует прибавить число 13. Итак, одноразрядный десятичный сумматор для деся­тичных разрядов, представленных в коде с избытком 3, описывается соотношениями:

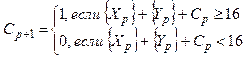
(6.6)

где C_p+1 — перенос в следующий десятичный разряд; {S_p} – значение р-го десятичного разряда суммы чисел X и Y; С_р = 0 или 1 – перенос из предыдущего десятичного разряда. Сложение с числами 3 и 13 называется коррекцией суммы. Из соотношения (6.6) видно, что вычисление суммы {Sp}можно вы­полнить с помощью двух последовательно включенных 4-разрядных двоичных сумматоров: первый сумматор вычисляет вспомогательную сумму

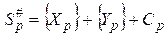и перенос С_p+1, а второй сумматор – сумму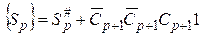

так как C_p+1 C_p+1 C_p+1 1 = 13 при С_р+1 = 0 и С_р+1C_p+1C_p+1 1 = 3 при C_p+1 = 1. Такое устройство называ­ется сумматором кодов с избытком 3.

Рассмотрим теперь вычитание n-разрядных десятичных чисел X и Y с использованием кода с избытком 3.

Так как S’=X-Y=X-10ⁿ+(10ⁿ-Y)= X-10ⁿ+W, где W=10ⁿ-Y,

То вычитание из X числа Y эквивалентно сложению X с дополнением Y до 10ⁿ с коррекцией результата на 10ⁿ.

При Х ³ 5 надо производить сложение числа Х (x₄, x₄, x₄, x₄) с числом 3. Таким образом, данный преобразователь выполняет функцию Y = X, если 0 £ Х £ 4 и Y = X + 3, если 5£ Х£ 9.

Таблица 6.3 Таблица истинности преобразователя

двоичного кода в двоично-десятичный

Построим преобразователь двоично-десятичного кода в двоичный на ЛЭ.

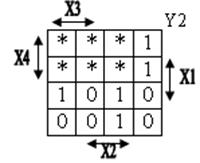
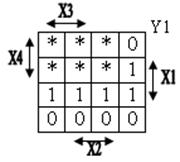
Для получения логических выражений представим переменные Y1, Y2, Y3, Y4 в форме таблиц Вейча:

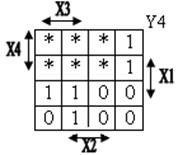
Тогда для Y4 можно записать: 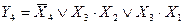, или иначе:

.

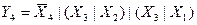Аналогично, для остальных Y:

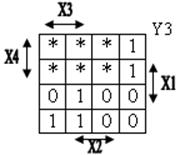
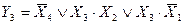
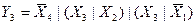
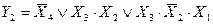
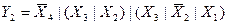
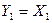
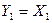
Теперь при помощи полученных логических выражений на элементах И-НЕ построим преобразователь двоичного кода в двоично-десятичный код (рис. 6.25).

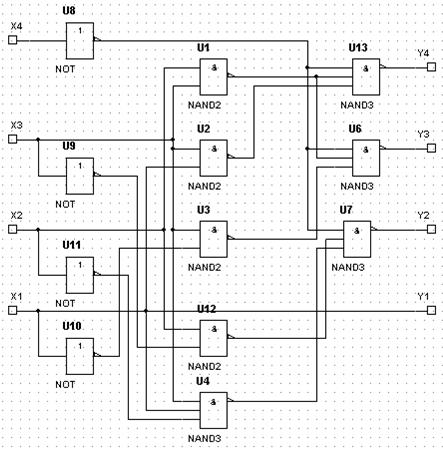
Рис. 6.25 Схема преобразователя двоичного кода в двоично-десятичный код

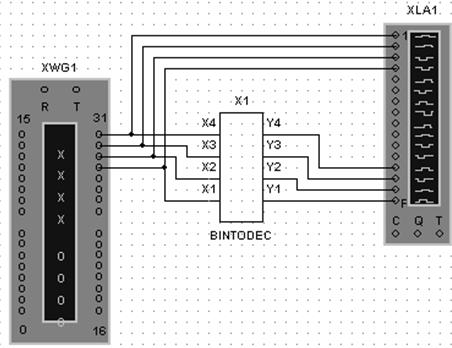
Рис. 6.26 Блок преобразователя двоичного кода в

двоично-десятичный код

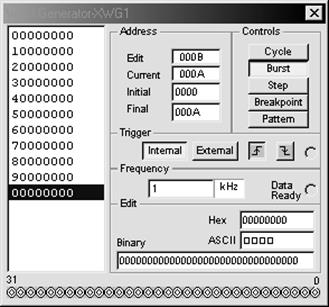
Рис. 6.27 Заданная последовательность входных сигналов

для схемы (рис. 6.20)

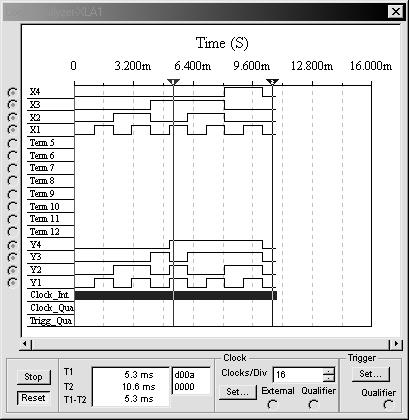
Рис. 6.28 Временные диаграммы для преобразователя двоичного кода в двоично-десятичный код

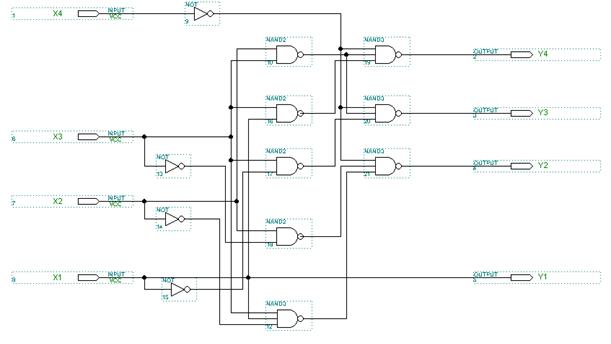
Рис. 6.29 Преобразователь двоичного кода в двоично-десятичный код в пакете MAX+Plus II

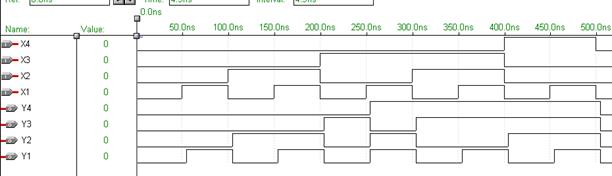
Рис. 6.30 Временные диаграммы

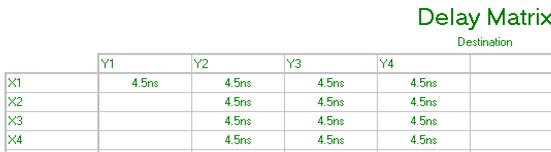
Рис. 6.31 Матрица временных задержек

Программа:

SUBDESIGN preobraz_dvoichnogo_v_dvoichno_desayt

(

X[3..0]: INPUT;

Y[3..0]: OUTPUT;

)

BEGIN

IF X[3..0] < = B" 0100"

THEN Y[3..0] = X[3..0];

ELSE Y[0] = X[0];

TABLE

X[3..1] => Y[3..1];

B" 010" => B" 101";

B" 011" => B" 110";

B" 100" => B" 111";

END TABLE;

ENDIF;

END;

Примечание. В пакете Max+ Plus2 имеются микросхемы, реализующие преобразование из двоичного кода в двоично-десятичный и обратно (74184/74185).