💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Преобразователь прямого кода в дополнительный код

При построении взаимных преобразователей кодов следует исходить из определений для этих кодов и правил взаимного преобразования (перевода).

Правила взаимного преобразования кодов вытекают из определений кодов и правил двоичной арифметики. В частности, х Å 0 = х, х Å 1 = х.

Общие правила взаимного преобразования кодов n-разрядных двоичных чисел можно выразить следующими соотношениями:

а) если необходимо [Х]^п/ [Х]⁰, то [X]⁰=(X_n+1, x^п_nÅ x_n+1, x^п_n-1Å x_n+1 , …, x^п₁Å x_n+1);

б) если необходимо [Х]⁰/ [Х]^п, то [X]^п=(X_n+1, x⁰_nÅ x_n+1, x⁰_n-1Å x_n+1 , …, x⁰₁Å x_n+1);

в) если необходимо [Х]^п/ [Х]^д, то [X]^д=[(X_n+1, x^п_nÅ x_n+1 , …, x^п₁Å x_n+1) Å x_n+1];

г) если необходимо [Х]^д/ [Х]^п, то [X]^п=[(X_n+1, x^д_nÅ x_n+1 , …, x^д₁Å x_n+1) Å x_n+1];

д) если необходимо [Х]⁰/ [Х]^д, то [X]^д = [Х]⁰ Å x_n+1 ,

где [X]^п – прямой код числа,

[X]^о – обратный код числа,

[X]^д – дополнительный код числа.

При использовании сумматора в качестве преобразователя кода необходимо иметь (n+1)-разрядный сумматор, причем на неиспользованные входы подают нуль, т.к. хÅ 0=х, а для формирования сигнала переноса (знакового разряда) используют (n+1)-й вход сумматора.

Например, построим преобразователь трехразрядных чисел прямого кода в дополнительный, т.е. осуществим [Х]п/[Х]д

При построении преобразователя будем руководствоваться алгоритмами в) и г). Из их анализа следует, что при преобразовании кодов необходимо вначале произвести поразрядно суммирование по модулю два входной информации (х3, x2, x1) и знакового разряда x4, а затем к полученному результату прибавить значение x₄. Первую операцию выполним с помощью n сумматоров по модулю 2 (схем " Исключающее ИЛИ"), а вторую - с помощью четырехразрядного сумматора. При этом результат суммирования по модулю 2 подадим поразрядно на один из входов сумматора, а на вторые (неиспользованные) входы подадим нуль. Знаковую информацию подадим на входы 4-го разряда сумматора и на вход переноса. Результат получим на выходах сумм, причем вход 4-го разряда будет знаковым.

Если на вход схемы преобразователя четырехразрядного прямого кода в дополнительный код (см. рис. 6.15) подать дополнительный код, то на выходе получим прямой код.

Подведём итог:

Правило кодирования: если число A> 0, то [A]_доп=[A]_пр, если число А< 0, то в знаковый разряд кода записывается 1, числовые разряды исходного числа инвертируются, и к младшему числовому разряду добавляется 1.

Например, число А = 1.111 в дополнительном коде

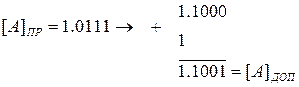
Схему такого преобразования можно собрать на сумматорах (рис.6.15).

В модифицированном дополнительном коде в отличие от дополнительного кода для представления знака числа отводится два разряда. Например, отрицательное число B, модуль которого равен 00.01110, в модифицированном дополнительном коде: [B]^M_доп = 11.10010.

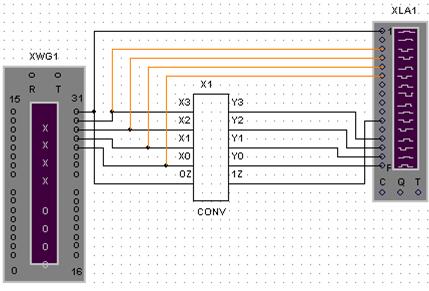
Рис. 6.14 Подключение преобразователя

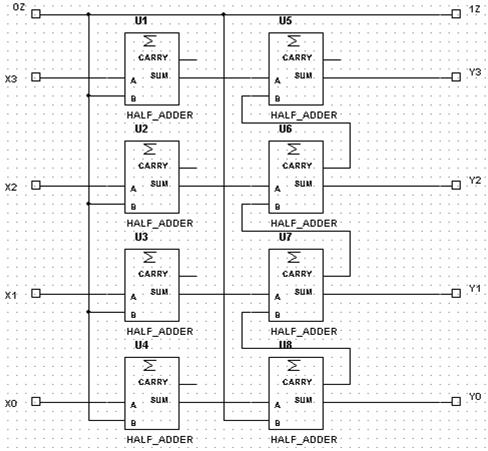
Рис. 6.15 Схема для преобразования прямого кода в дополнительный (для 4-х разрядных чисел)

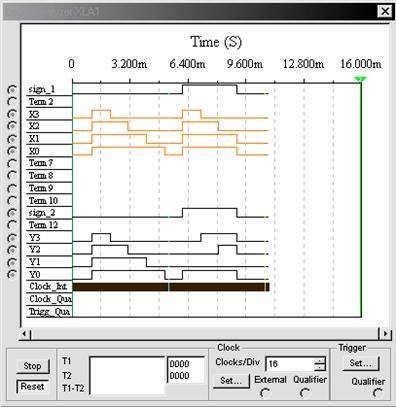
Рис. 6.16 Временные диаграммы для преобразователя прямого кода

в дополнительный

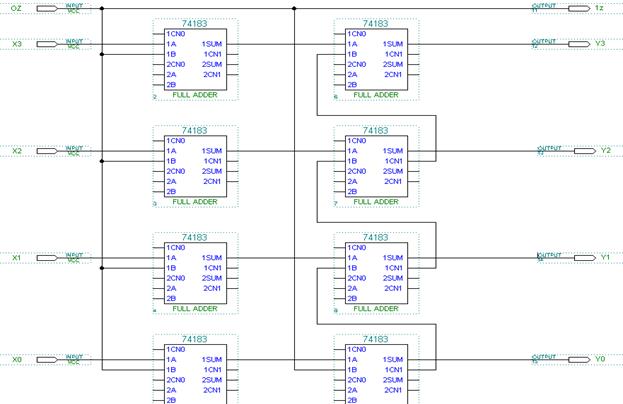
Рис. 6.17 Преобразователь прямого кода в дополнительный в пакете MAX+Plus II

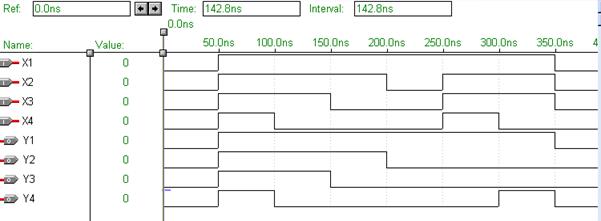
Рис. 6.18 Временные диаграммы для преобразователя прямого кода в дополнительный

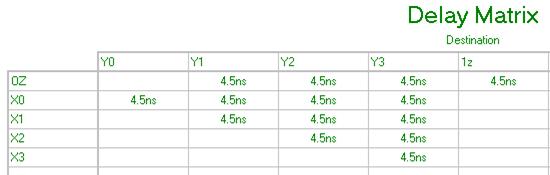
Рис. 6.19 Матрица временных задержек

Программа:

SUBDESIGN preobraz_praymogo_v_dopol

(X[3..0]: INPUT;

Y[3..0]: OUTPUT;

Q[3..0], t[3..0]: NODE;

)

BEGIN

IF x[3] == 0 THEN

Y[3..0] = x[3..0];

ELSE

t[3] = x[3];

t[2..0] =! x[2..0];

Q[3..0] = t[3..0] + B" 00000001";

y[3..0] = Q[3..0];

ENDIF;

END;

Обратите внимание, на временных диаграммах показаны не все возможные входные сигналы. Вам так же не рекомендуется перебирать их все (32 шт.). На временных диаграммах видно, что:

Такие комбинации были выбраны потому, что их очень легко проверить.