Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Решение. 3. Диэлектрическая пластина шириной 2а с ε=2 помещена в однородное электрическое поле Е, линии которого перпендикулярны пластине.
|
|
E = f(1/ε) D = ε 0ε E → D ≠ f(ε) → D1 = D2 = const
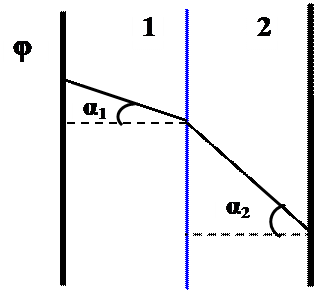
α 2 > α 1 → ε 1 – диэлектрик,
ε 2 – вакуум
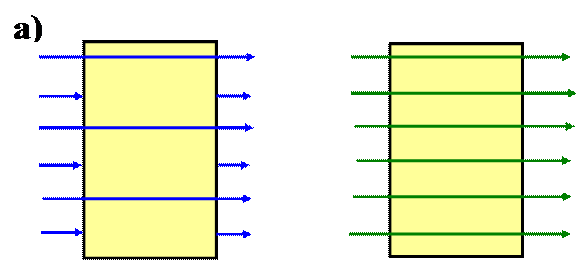
3. Диэлектрическая пластина шириной 2 а с ε =2 помещена в однородное электрическое поле Е, линии которого перпендикулярны пластине.
а) Изобразить на рисунке линии Е и D
б) Построить качественно графики зависимостей Ех и Dx
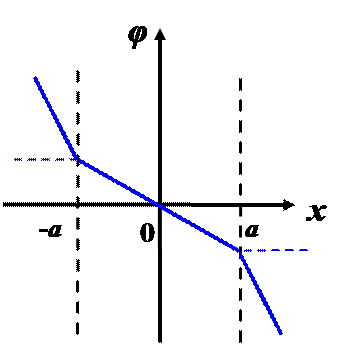
в) Построить качественно график зависимости потенциала φ от х.
Ось х перпендикулярна пластине, вектор Е направлен вдоль х, точка х=0 находится на середине ширины пластины).
В)
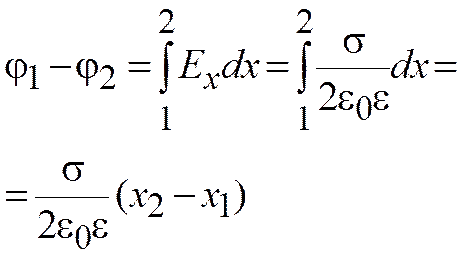
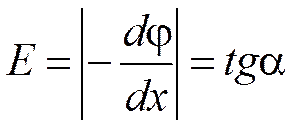
4. Указать верную подпись:
1) линии D, ε 1> ε 2
2) линии D, ε 1< ε 2
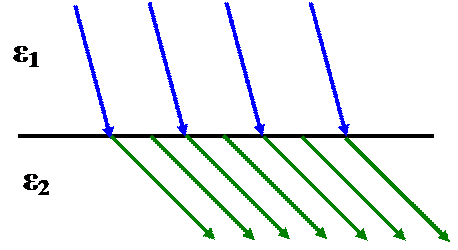3) линии Е, ε 1> ε 2
4) линии Е, ε 1< ε 2
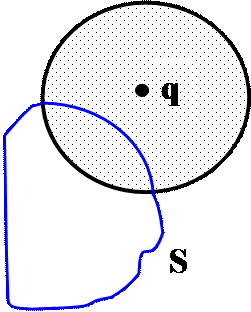
5. В поле точечного заряда q> 0 находится палочка из диэлектрика. Выделены 3 сферические области S1, S2, S3, в центре которых находится заряд q.
1) Сравнить потоки вектора Е через эти поверхности.
2) Сравнить потоки вектор D через эти же поверхности.
3) Можно ли найти D(r), используя теорему Гаусса?
1) NE1 = NE3 > NE2
2) ND1 = ND2 = ND3
3) Палочка нарушает сферическую
симметрию, поэтому D(r) с помощью
теоремы Гаусса определить нельзя.
6. Рассмотрим т.А вблизи заряда +q. Изменятся ли Е и φ в т.А, если заряд q и т.А окружить сферическим слоем диэлектрика с центром в точке, где находится заряд q? Варианты ответа: 1) Да; 2) Нет.
|
1) Через т. А проведем гауссову поверхность в виде сферы с центром, где находится +q. Поэтому Е поля в т. А не меняется.
2) Потенциал φ поля в т.А уменьшается. Это можно показать различными способами:
а) Используем принцип суперпозиции.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В результате поляризации возникают связанные заряды: -q′ и +q′. Т.о ., φ А = φ q – φ ′ - + φ ′ +
φ = f(1/r), поэтому /φ ′ -/ ≥ /φ `+/. Т.о., φ А уменьшается.
б) 
- определение потенциала. q′ φ 1∞ =A1∞ = F S = q′ ES.
, где F0 – сила в вакууме, F – сила в среде ε. Т.о., работа, а значит, и потенциал в т.А
уменьшается.
в) Эту задачу можно решить, используя связь между Е и φ: 
Кривая 1 (красного цвета) соответствует полю точечного заряда в вакууме 
. E = f(1/ε) - в среде.
Кривая 2 (синего цвета) – поле точечного заряда, окруженного слоем диэлектрика (внутри слоя Е уменьшается в ε раз). φ А определяется площадью под кривой E(r), исходя из геометрического смысла интеграла: 
Сравнивая площади под кривыми 1 и 2, приходим к выводу, что φ А уменьшается.
7. В центре сферической поверхности находится точечный заряд q. Изменится ли поток вектора D через поверхность, если а) все пространство заполнить диэлектриком; б) заменить сферическую поверхность кубической?
8. Вокруг точечного заряда q в диэлектрике с полярными молекулами проведена сфера. Как изменятся NE и ND через сферу, если а) диэлектрик нагреть; б) увеличить плотность вещества?
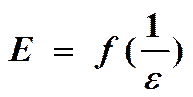; D ≠ f(ε); 
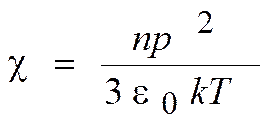- для полярного диэлектрика; ε = 1 +χ.
а) Е уменьшается в диэлектрике, поэтому из теоремы Гаусса следует: NE увеличивается, а ND не изменяется.
б) n – концентрация. Если увеличить n, то и ε увеличится и NE уменьшается, ND не
изменяется.
9. Точечный заряд q находится в центре диэлектрического шара. Отличны ли от нуля интегралы: 
по замкнутой поверхности S, частично захватывающей диэлектрик?
10. Имеется однородный равномерно и положительно заряженный по объему шар. Как изменяется поток вектора Е через единицу площади сферы, концентрической с шаром, при увеличении ее радиуса, если она располагается: 1) внутри шара; 2) снаружи (ε = 1)?
11. Дан бесконечно длинный цилиндрический равномерно заряженный по объему диэлектрический стержень. Определить зависимость потока вектора Е сквозь мысленно построенную цилиндрическую поверхность от ее радиуса r, если эта поверхность соосна со стержнем и проходит внутри его. Диэлектрик однородный.
Варианты ответа: 1) N ~ r; 2) N ~ r2;
3) N ~ r -1; 4) N = const.
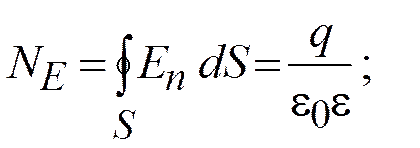
12.
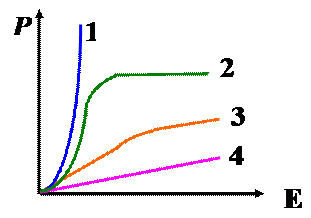На рисунке представлены графики отражающие характер зависимости поляризованности диэлектрика от напряженности Е. Укажите зависимость соответствующую различным типам диэлектриков.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|