Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Гауссовой поверхности

ЭЛЕКТРОСТАТИКА (ПРАКТИКА)

ТЕОРЕМА ГАУССА

;

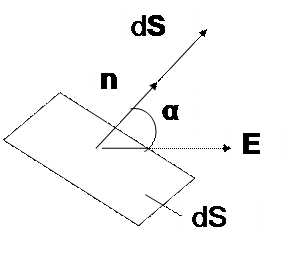
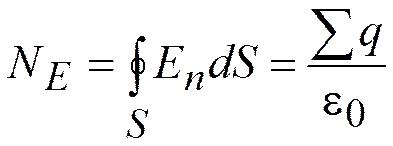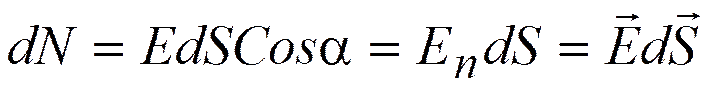
Поток вектора Е сквозь произвольную поверхность S: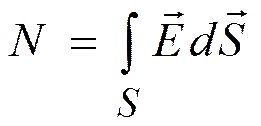

Алгоритм применения теоремы

1) Сформулировать и записать математическое выражение теоремы.

2) Сделать рисунок распределения заряда и определить тип симметрии.

3) Изобразить на рисунке силовые линии электрического поля.

4) Выбрать и нарисовать гауссову поверхность.

5) Записать выражение для потока N через построенную поверхность.

6) Найти заряд q, находящийся внутри объема, ограниченного гауссовой поверхностью.

7) Подставить выражения для N и q в формулу теоремы, найти Е.

Требования к построению

гауссовой поверхности

1. Форма S должна соответствовать типу симметрии распределения заряда.

2. Поверхность S должна проходить через точку, в которой требуется определить поле.

3. На S или ее части напряженность Е поля должна быть направлена по нормали и принимать одинаковые значения Е = Е_n = const или нормальная составляющая

E_n = 0.

1. Можно ли применить для вычисления потока вектора Е формулу N = ES в случаях:

1) поверхность цилиндрическая, вдоль ее оси направлена бесконечная равномерно заряженная нить;

2) поверхность цилиндрическая, на ее оси находится заряженная равномерная нить АВ, длина которой соизмерима с высотой цилиндра;

3) поверхность - основание указанного выше цилиндра.

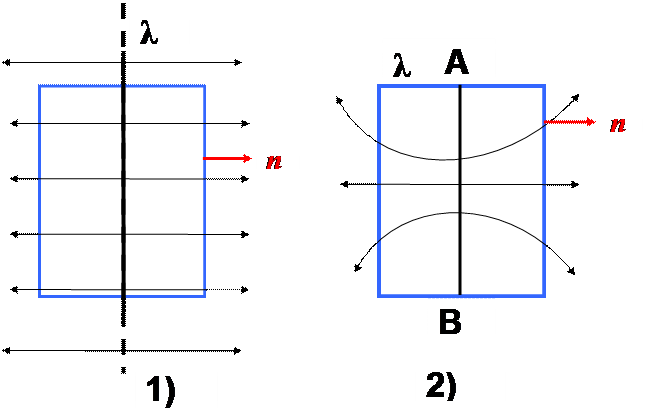
1) В этом случае поле обладает радиальной симметрией. Поэтому на боковой цилиндрической поверхности цилиндра Е = Е_n = const, формулу N = ES можно применять.

Для основания цилиндра в этом случае

Е_n = 0, т.е. данную формулу применить

нельзя (3).

2) В случае конечной длины нити на боковой цилиндрической поверхности цилиндра → .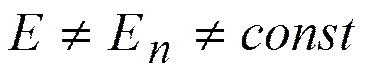

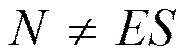Для основания цилиндра в этом случае 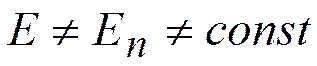, т.е. данную формулу применить нельзя (3).

2. Точечный заряд + q находится в центре сферической поверхности. Если добавить заряд + q за пределами сферы то поток вектора Е через поверхность сферы…

Варианты ответа: 1) не изменится; 2) увеличится; 3)уменьшится.

3. Дана система точечных зарядов в вакууме и замкнутые поверхности S ₁, S ₂ и S ₃. Поток вектора Е электростатического поля отличен от нуля через поверхности…

Варианты ответа: 1) S ₁; 2) S ₂; 3) S ₃.

4. Симметричное сферическое облако ионизированных частиц расширяется. Изменяются ли: 1) поток вектора напряженности N через поверхность облака, 2) напряженность поля на границе облака?

5. Найти напряженность поля, созданного бесконечным слоем с внутренним радиусом R₁ и внешним - R₂ , заряженным с постоянной объемной плотностью ρ.

;

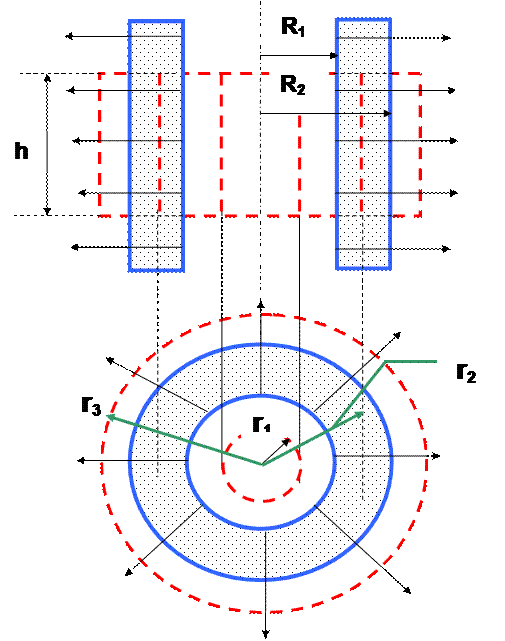
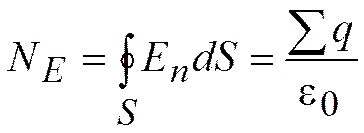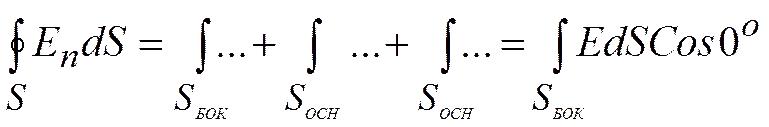
ρ = q /V

1. r₁ < R₁

q = 0 → E₁ = 0

2. R₁ < r₂ < R₂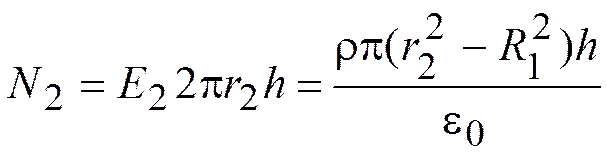

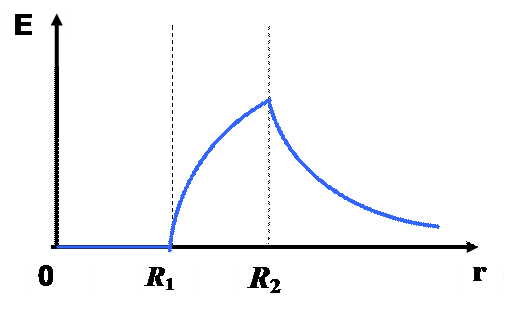
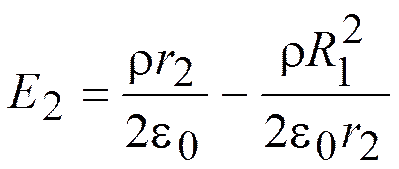
3. r₃ > R₂

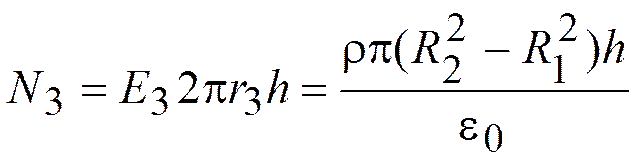
6.

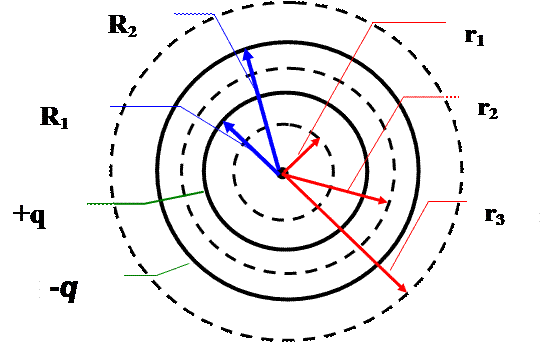Cферический конденсатор представляет собой две концентрические сферы радиусов R ₁ и R ₂ (R ₁< R ₂). Заряды на внутренней и внешней сферах равны соответственно + q и – q. Определить Е и φ внутри сферы радиуса R ₁, между сферами и вне сфер.

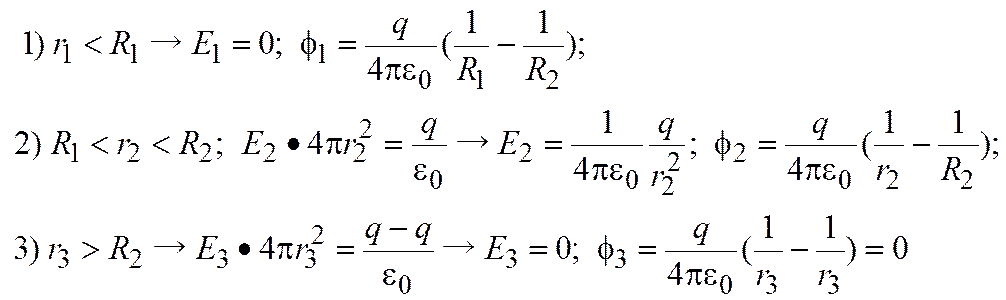
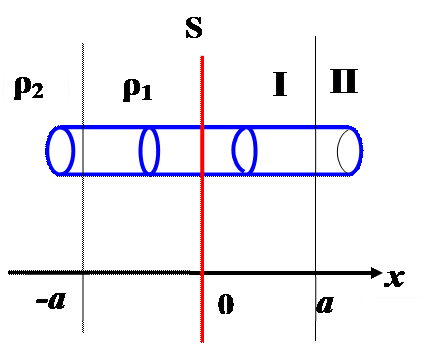
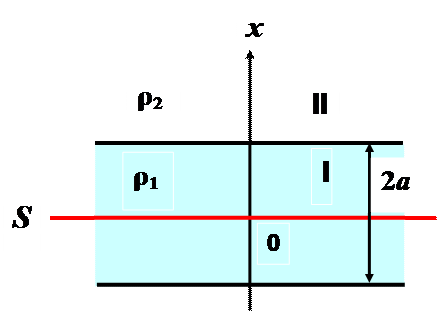7. Заряд распределен симметрично относительноплоскости S таким образом, что его объемная плотность зависит от координаты х, отсчитываемой от плоскости симметрии, по закону:

r₁ = r₀ при | x | < a;

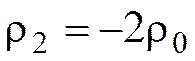при | x | > a.

1) Используя теорему Гаусса, найти зависимость E (x) напряженности электростатического поля от координаты x для областей I, II. Принять r₀ = 0, 1 мкКл/м³, a = 2 м;

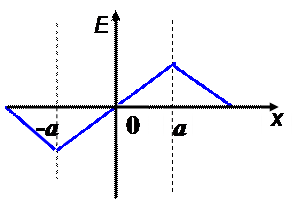
2) построить график E(x).
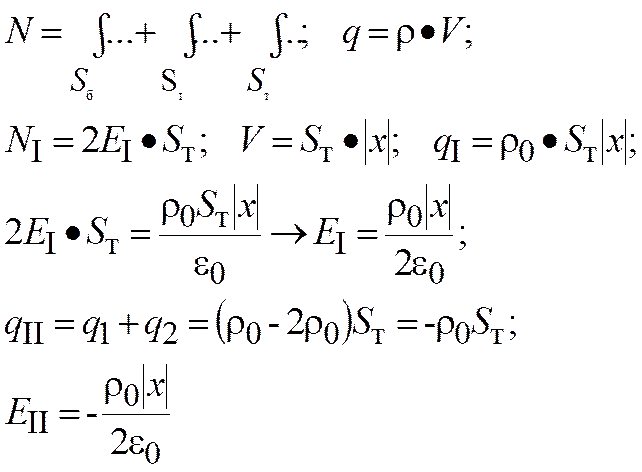