Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет токов, охватываемых контуром интегрирования
|
|
1) I = Σ Ii – линейные токи;
2) I = ∫ i∙ dl – поверхностные токи, где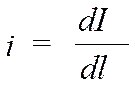 
- линейная плотность тока;
3) I = ∫ j dS – объемные токи, где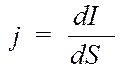 
- поверхностная плотность тока.
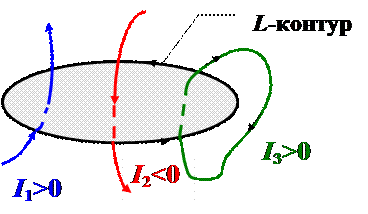Ток считается положительным I > 0, если его направление связано с направлением обхода по контуру правилом правого винта. И наоборот, отрицательным I < 0.
Магнитное поле сплошного цилиндра радиуса R, по которому протекает однородный ток равномерно распределенный по сечению плотностью j: j = const
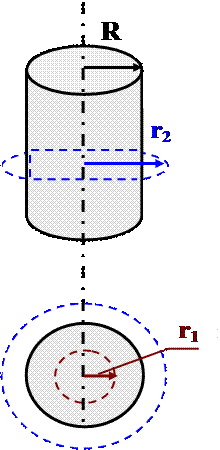
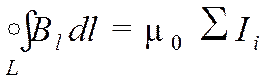
j – поверхностная плотность тока, т.к. ток – объемный
1) r 1 < R: I = j . π r 12
B 1.2π r1 = µ0 j ∙ π r12 → B 1 = ½ µ0 j ∙ r 1
2) r 2 > R I = j ∙ π R 2
B2 2π r2 = µ0 j∙ π R2 →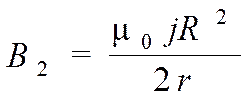 
Теорема о циркуляции вектора Н
(Закон полного тока для магнитного поля в веществе)
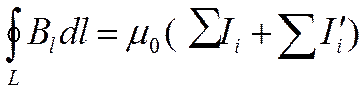(1) - теорема о циркуляции вектора В в веществе,
Σ Ii – сумма токов проводимости; Σ Ii ′ - cумма токов намагничивания (микротоков).
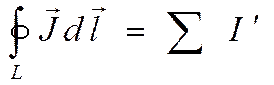(2) – циркуляция вектора намагничивания J. (2) → (1) →
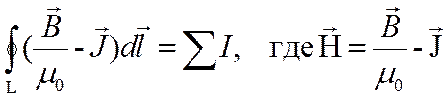- определение напряженности Н.
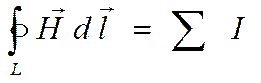– циркуляция вектора Н равна алгебраической сумме токов проводимости, охватываемых контуром.
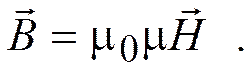
1. Какова циркуляция вектора напряженности магнитного поля по контуру, изображенному на рисунке? I 1 = 2A, I 2 = 5A.
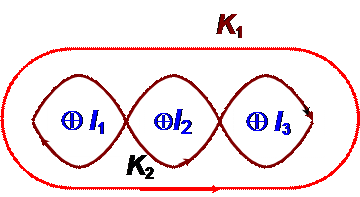2. Определить циркуляцию вектора напряженности по контурам K 1 и K 2. I 1= I 2 = I 3 = 1A.
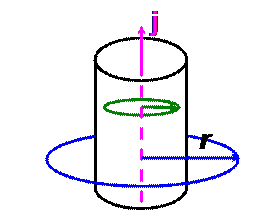3. По бесконечно длинному прямолинейному проводу течёт ток с плотностью, равномерно распределенной по сечению. Как изменяется модуль циркуляции вектора напряженности магнитного поля по круговому контуру с центром на оси провода при увеличении радиуса контура, если он располагается: а) внутри провода; б) вне провода?
4. Изменится ли циркуляция вектора магнитной индукции В по контуру, охватывающему проводник с током, если а) пространство заполнить однородным и изотропным магнетиком; б) добавить ток за пределами контура; в) контур деформировать.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
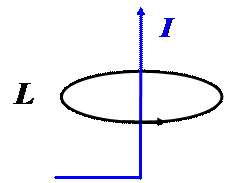5. Для кругового контура длиной l, охватывающего бесконечно длинный проводник с током I, идущим по оси контура, справедливы соотношения:
a)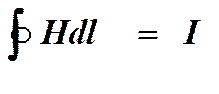 
; б)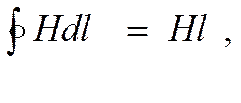 
где Н – модуль напряженности магнитного поля в произвольной точке контура. Справедливы ли эти выражения для контура L, если провод согнут под прямым углом (Рис.)?
|
|