Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задачи выпуклого программирования

Пусть исходная задача имеет вид:

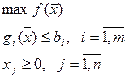
Задача (11-13) называется задачей выпуклого программирования, если выполняются следующие условия:

1. 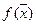– вогнутая функция, то есть для .

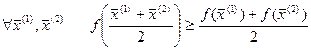2. Область допустимых решений 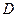выпуклая.

3. Область регулярная, то есть существует по крайней мере одна внутренняя точка .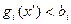

Можно построить функцию Лагранжа

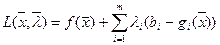
Теорема 8: точка 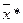является оптимальным решением задачи выпуклого программирования тогда и только тогда, когда существует вектор 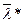такой, что для функции Лагранжа выполняются условия

1.

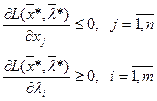
2. условия дополняющей нежесткости:

3.

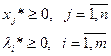
Условия (14) называются условиями Куна-Таккера, а точка 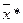– точкой Куна-Таккера

Рассмотрим геометрический смысл условий Куна-Таккера.

Из первого условия (14.2) следует, что если все 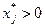, , 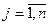то

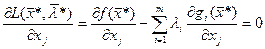
Второе условие (14.2), так как 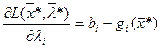, запишется в виде

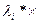
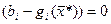
и означает, что для неактивных ограничений .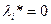

Тогда из условий дополняющей нежесткости следует

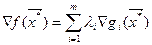(15)

то есть градиент функции 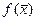в оптимальной точке является линейной комбинацией с положительными коэффициентами градиентов к активным ограничениям. Иными словами, градиент критерия лежит в геометрическом конусе градиентов ограничений.

Если в оптимальной точке какая-либо координата 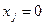, то вместо градиентов функци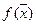й и 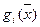рассматриваются их проекции на плоскость, перпендикулярную оси .

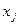В общем случае система уравнений и неравенств (14) слишком сложна для аналитического решения. Однако в задачах квадратичного программирования есть способы решения этой системы условий, сводящиеся к нахождению опорных решений систем линейных алгебраических уравнений.