
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи на условный экстремум. Метод множителей Лагранжа.
|
|
Задача на условный экстремум ставится как задача определения управляемых параметров
|
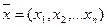 , на которых достигается экстремум (максимум или минимум) при ограничениях, заданных уравнениями.
, на которых достигается экстремум (максимум или минимум) при ограничениях, заданных уравнениями.
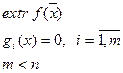
Задачу на условный экстремум можно свести к задаче на безусловный экстремум для специальным образом построенной функции.
Каждому ограничению поставим в соответствие переменную 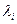 .
.
Построим функцию Лагранжа:
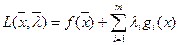
Если ограничения выполняются, то функция Лагранжа превращается в исходную функцию.
Точки локальных экстремумов задачи (8), (9) будут точками локальных экстремумов функции Лагранжа.
Теорема 6 (необходимое условие экстремума): если 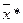 – точка локального экстремума и в окрестности этой точки функции
– точка локального экстремума и в окрестности этой точки функции  непрерывно дифференцируемы, то в этой точке выполняются условия
непрерывно дифференцируемы, то в этой точке выполняются условия
|
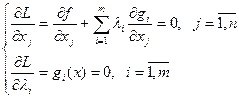
Условия (10) означают, что градиент функции Лагранжа равен нулю
|
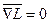
Для формулировки достаточных условий оптимальности рассмотрим
окаймляющую матрицу Гессе:
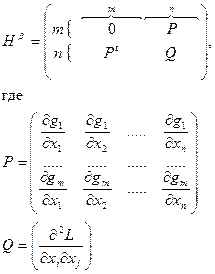
Теорема 7 (достаточное условие экстремума):
· Стационарная точка функции Лагранжа 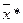 является точкой локального минимума, если в окаймляющей матрице Гессе, вычисленной в стационарной точке, все угловые миноры, начиная с порядка
является точкой локального минимума, если в окаймляющей матрице Гессе, вычисленной в стационарной точке, все угловые миноры, начиная с порядка 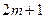 имеют знаки, определяемые множителем
имеют знаки, определяемые множителем 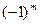 .
.
· Стационарная точка функции Лагранжа 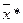 является точкой локального максимума, если все угловые миноры окаймляющей матрицы Гессе, начиная с
является точкой локального максимума, если все угловые миноры окаймляющей матрицы Гессе, начиная с 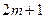 порядка образуют знакопеременный ряд, в котором знак первого члена определяется множителем
порядка образуют знакопеременный ряд, в котором знак первого члена определяется множителем 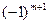 .
.
Достаточное условие оптимальности можно сформулировать также в другой форме: если рассмотреть определитель, построенный из окаймляющей матрицы Гессе
|
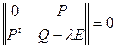 ,
,
то стационарная точка функции Лагранжа является точкой максимума, если все  действительных корней многочлена (11) меньше ноля. Если же корни больше нуля, стационарная точка функции Лагранжа является точкой минимума.
действительных корней многочлена (11) меньше ноля. Если же корни больше нуля, стационарная точка функции Лагранжа является точкой минимума.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пример: Предприятие выпускает два вида продукции в объемах 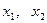 . Они реализуются по ценам
. Они реализуются по ценам 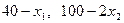 соответственно. По плану предприятие должно выпустить ровно 50 единиц продукции. Определить план производства, обеспечивающий наибольший доход.
соответственно. По плану предприятие должно выпустить ровно 50 единиц продукции. Определить план производства, обеспечивающий наибольший доход.
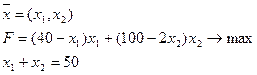
Здесь функция ограничений
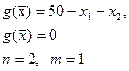
Построим функцию Лагранжа
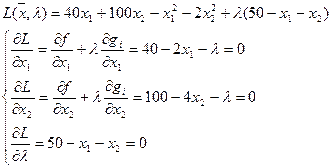
Вычитая из второго уравнения первое, получим
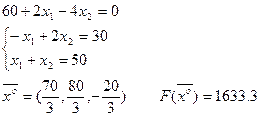
Проверим достаточное условие оптимальности:
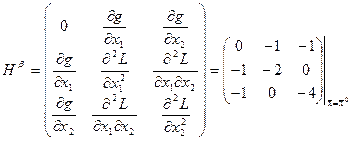
Угловые миноры матрицы, начиная с порядка 2 m +1=3 должны иметь чередующиеся знаки, знак первого из них 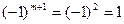 (положителен). Все эти условия выполняются:
(положителен). Все эти условия выполняются:

Полученное решение – точка локального максимума.
Экономическая интерпретация множителей Лагранжа
Множитель Лагранжа 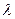 – это двойственная переменная. Как и в линейном программировании, она показывает, на сколько изменится критерий при изменении правой части ограничений на единицу.
– это двойственная переменная. Как и в линейном программировании, она показывает, на сколько изменится критерий при изменении правой части ограничений на единицу.
В рассмотренном примере 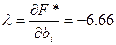 . Следует ожидать, что при увеличении суммарного объема производимой продукции с 50 до 51 доход уменьшится на 6.66.
. Следует ожидать, что при увеличении суммарного объема производимой продукции с 50 до 51 доход уменьшится на 6.66.
Проверим этот вывод. Пусть в нашей задаче критерий остался прежним, поменялась правая часть ограничения
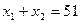 .
.
Тогда условия стационарности выглядят следующим образом:
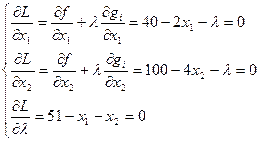
Стационарная точка
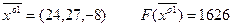
Приращение критерия
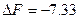
Для проверки достаточного условия оптимальности найдем корни многочлена, построенного из окаймляющей матрицы Гессе:
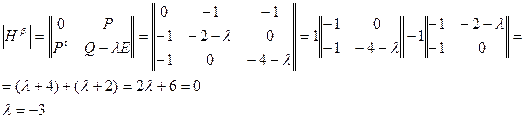
Корень отрицательный, значит это точка максимума функции.
Приращение функции -7.33 оказалось больше по модулю, чем ожидаемое приращение -6.66. Это объясняется нелинейностью целевой функции и тем, что производная 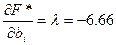 отражает приращение функции только при бесконечно малом приращении аргумента.
отражает приращение функции только при бесконечно малом приращении аргумента.
|
|
