
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа 13
|
|
СТАЦИОНАРНЫЕ ПРОЦЕССЫ В ДЛИННОЙ ЛИНИИ
Цель работы: исследование стационарных гармонических колебаний в длинной линии и различных режимов ее работы.
РАСЧЕТНЫЕ СООТНОШЕНИЯ
Свойства длинной линии определяются ее распределенными (погонными) параметрами: погонной индуктивностью L0 (Гн/м), погонной емкостью C0 (Ф/м), погонным активным сопротивлением потерь R0 (Ом/м) и погонной проводимостью утечки G0 (Сим/м). Их часто называют первичными.
Комплексная амплитуда напряжения Um(x) и тока Im(x) на расстоянии x от конца (нагрузки) длинной линии определяется системой " телеграфных" уравнений вида:
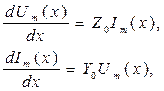
где Z0 = R0 + jwL0, Y0 = G0 + jwC0, w - частота колебаний.
Волновые процессы в длинной линии характеризуются коэффициентом (постоянной) распространения g = a + jb, где a - коэффициент затухания, а b - коэффициент фазы.
Волновое (характеристическое) сопротивление Zс длинной линии определяется соотношением
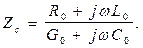
Фазовая скорость Vф перемещения точки фиксированной фазы падающей или отраженной волны вдоль линии равна
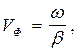
а коэффициент фазы связан с длиной волны колебаний l в линии выражением
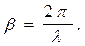
Для длинной линии без потерь выполняются равенства:
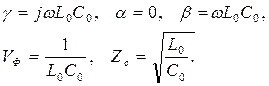
Эти выражения приближенно справедливы и в длинной линии с потерями при условии R0 < < wL0, G0 < < wC0.
Соотношение между амплитудами стоячей и бегущей волн в длинной линии характеризуется коэффициентом бегущей волны (КБВ)
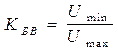
или коэффициентом стоячей волны (КСВ)
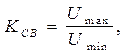
где Umin и Umax - соответственно наименьшая и наибольшая амплитуды напряжения вдоль линии.
В длинной линии без потерь при активной нагрузке Rн можно записать
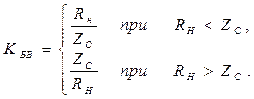
Входное сопротивление Zвх линии в этом случае определяется выражением
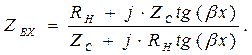
При Rн=Zс (в режиме бегущих волн) входное сопротивление линии равно характеристическому Zвх=Zс, а, например, при коротком замыкании линии (Rн=0) входное сопротивление реактивно и равно
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
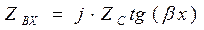 .
.
При подключении к длинной линии реактивной нагрузки происходит смещение узлов и пучностей напряжения и тока вдоль линии. Если, например, в короткозамкнутой линии вместо замыкателя подключить индуктивность L, то узлы и пучности сместятся ближе к нагрузке на расстояние
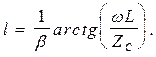
Полученное выражение следует из того, что индуктивность L можно заменить отрезком короткозамкнутой линии длиной l.
Волновое сопротивление двухпроводной длинной линии, размещенной в вакууме (в воздухе) равно
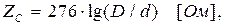
где d -радиус проводов линии, D - расстояние между центрами проводов линии.
ЛАБОРАТОРНАЯ УСТАНОВКА
Пятиметровая двухпроводная длинная линия укреплена на растяжках, вмонтированных в противоположные стены лаборатории (рис. 45). С одной стороны с ней соединен генератор высокочастотных гармонических сигналов e(t), а с другой подключается нагрузка Zн. Для измерения расстояний вдоль линии укреплена линейка.
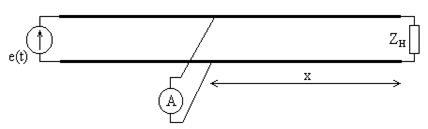 Рис. 45. Лабораторная установка
Рис. 45. Лабораторная установка
Измерение напряжения между проводами линии производится подвесным стрелочным индикатором A, перемещаемым электромеханическим приводом.
ДОМАШНЕЕ ЗАДАНИЕ
Рассчитайте волновое сопротивление лабораторной длинной линии с диаметром провода 3 мм и с расстоянием между ними 220 мм.
Начертите кривые изменения амплитуды тока и напряжения от расстояния от конца линии (нагрузки) для случаев:
а) линии, разомкнутой на конце;
б) линии, замкнутой на конце;
в) линии, замкнутой на активное сопротивление, равное волновому;
г) линии, замкнутой на активное сопротивление, большее волнового;
д) линии, замкнутой на активное сопротивление, меньшее волнового.
Изложите методику практического определения с помощью длинной линии неизвестного активного сопротивления, полагая заданным ее волновое сопротивление.
ЛАБОРАТОРНОЕ ЗАДАНИЕ
1. Подготовьте длинную линию к работе. Для этого включите генератор высокочастотного сигнала, перемещая индикатор вдоль линии, убедитесь в наличии в ней колебаний, отключите нагрузку, обеспечив режим холостого хода.
2. Перемещая индикатор, измерьте длину волны колебаний в линии, определите частоту генератора.
3. В режиме холостого хода на участке линии, равном длине волны, снимите зависимость показаний индикатора А от расстояния x от конца линии. Измерения начинайте на расстоянии 80 см от нагрузки и перемещайте индикатор с шагом 10 см по направлению к генератору.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Результаты занесите в табл. 29. Определите максимальное значение показаний индикатора Amax, вычислите величины нормированного напряжения U = A/Amax и внесите их в табл. 30. Постройте график зависимости U(x). Определите коэффициент бегущей волны КБВ.
Таблица 29
Результаты измерения напряжения вдоль линии при ZH=…
| KБВ=… | x | ||||||
| A | |||||||
| U |
4. Проделайте измерения по предыдущему пункту для:
а) линии, замкнутой на конце;
б) линии, замкнутой на активное сопротивление, равное волновому;
в) линии, замкнутой на активное сопротивление, большее волнового;
г) линии, замкнутой на активное сопротивление, меньшее волнового.
Результаты оформите в таблицах, аналогичных табл. 29.
5. На основании измерений в пунктах 4в и 4г определите величину сопротивления нагрузки, считая его неизвестным. Сравните результаты с номинальными значениями нагрузки. Измерьте величины сопротивлений на постоянном токе, сравните результаты.
6. Подключите к линии в качестве нагрузки емкость C. Измерьте смещения узлов и пучностей по отношению к замкнутой и разомкнутой на конце линии. По результатам измерений определите величины емкости, найдите ее среднее значение, сравните результаты с номинальным значением.
ДЛЯ ПЫТЛИВЫХ
Проведите измерения пункта 6 для подключенной в качестве нагрузки неизвестной индуктивности.
МОДЕЛИРОВАНИЕ
Моделирование токов и напряжений в различных точках длинной линии в пакете MicroCAP не предусмотрено. С его помощью можно исследовать линию передачи как четырехполюсник во временной области в режиме “Transient analysis” или в частотной области в режиме “AC Analysis”.
Проведите расчет погонных параметров используемой в работе линии и введите их в программу моделирования.
Проведите анализ временных диаграмм сигналов на входе и выходе линии, ее частотные характеристики.
КОНТРОЛЬНЫЕ ЗАДАЧИ
1. Используя данные табл. 30, определите амплитуды напряжения 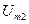 и тока
и тока 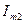 в точке, расположенной на расстоянии x от конца линии, N - номер варианта,
в точке, расположенной на расстоянии x от конца линии, N - номер варианта, 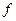 - частота сигнала,
- частота сигнала, 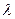 - длина волны,
- длина волны, 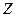 - волновое сопротивление.
- волновое сопротивление.
Таблица 30
| N | 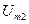 ,
В ,
В
| 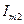 ,
А ,
А
| Режим в конце линии | f, МГц | 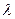 ,
м ,
м
| x, м | 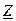 ,
Ом ,
Ом
|
| - | разомкнута | - | 2, 5 | ||||
| - | 1, 5 | замкнута | - | 1, 25 | |||
| - | разомкнута | - | |||||
| - | 0, 5 | замкнута | - | 2, 5 | |||
| - | разомкнута | - |
2. Используя данные табл. 31, определите наименьшую длину короткозамкнутой либо разомкнутой линии, 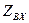 - входное сопротивление.
- входное сопротивление.
Таблица 31
| N | Режим в конце линии | 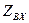 ,
Ом ,
Ом
| 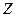 ,
Ом ,
Ом
| 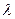 ,
м ,
м
| f, МГц |
| замкнута | -j80 | - | |||
| разомкнута | j60 | - | |||
| замкнута | j140 | - | |||
| разомкнута | -j120 | . | |||
| замкнута | j125 | - |
Примеры решения задач
3. Амплитуда напряжения в конце разомкнутой линии равна 100 В, частота колебаний 100 МГц, волновое сопротивление линии 100 Ом. Определите амплитуды напряжения и тока в точке, находящейся от конца линии на расстоянии 0, 5 м.
Решение
Известно, что в разомкнутой линии амплитуды напряжений и тока вдоль линии распределены по законам
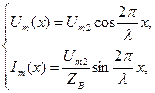
где x – расстояние от заданной точки до конца линии.
Подставляя в систему уравнений данные условия задачи, получим
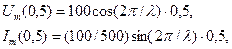
где 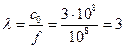 м,
м,
тогда
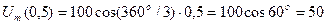 В,
В,
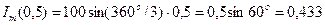 А.
А.
4. Рассчитайте минимальные длины короткозамкнутой и разомкнутой линии, входные сопротивления которых носят индуктивный характер и равны 100 Ом каждое при 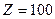 Ом,
Ом, 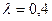 м.
м.
Решение
Входное сопротивление короткозамкнутой линии определяется из формулы
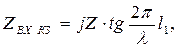
а входное сопротивление разомкнутой линии
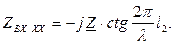
Из условия задачи имеем
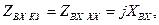
тогда
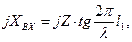
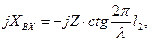
или
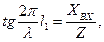
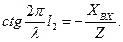
Из первого уравнения получаем
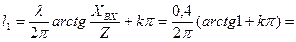
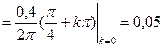 м.
м.
Из второго уравнения находим
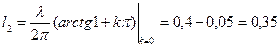 м.
м.
5. На конце линии с волновым сопротивлением 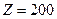 Ом включена емкость
Ом включена емкость 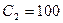 пФ. Определите место нахождения узла напряжения, ближайшего к концу линии, если
пФ. Определите место нахождения узла напряжения, ближайшего к концу линии, если 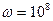 1/с.
1/с.
Решение
Подключение емкости равносильно “удлинению” линии на величину l, определяемую из соотношения
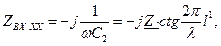
где 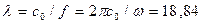 м при скорости света
м при скорости света 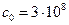 м/c, тогда получим
м/c, тогда получим
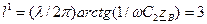 м.
м.
В разомкнутой линии узел напряжения находился бы на расстоянии 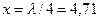 м, а емкость
м, а емкость 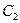 смещает узел к концу линии на расстояние
смещает узел к концу линии на расстояние 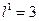 м. Следовательно, ближайший узел напряжения будет находиться на расстоянии
м. Следовательно, ближайший узел напряжения будет находиться на расстоянии 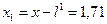 м.
м.
6. Амплитуда падающей волны напряжения в линии равна 100 В, коэффициент отражения в конце линии 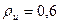 . Волновое сопротивление линии – 100 Ом. Определите амплитуду отраженной волны напряжения, а также максимальные и минимальные значения амплитуды напряжения в линии и коэффициент бегущей волны.
. Волновое сопротивление линии – 100 Ом. Определите амплитуду отраженной волны напряжения, а также максимальные и минимальные значения амплитуды напряжения в линии и коэффициент бегущей волны.
Решение
Амплитуда отраженной волны напряжения равна
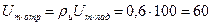 В.
В.
Максимальная амплитуда в пучности напряжения равна
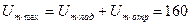 В,
В,
а минимальная амплитуда в узле напряжения равна
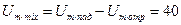 В.
В.
Тогда коэффициент бегущей волны (КБВ) равен
КБВ= 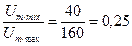 .
.
7. Длинная линия с волновым сопротивлением 500 Ом нагружена на активное сопротивление. Наибольшая амплитуда напряжения в линии равна 100 В, а наименьшая – 50 В. Определите возможные величины сопротивления нагрузки.
Решение
Известно, что КБВ определяется соотношением
КБВ= 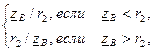
Следовательно
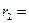
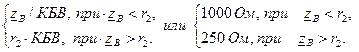
|
|
