
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение Больцмана.
|
|
При рассмотрении распределения Максвелла полагалось, что внешние силовые поля отсутствуют. Рассмотрим случай, когда идеальный газ находится во внешнем силовом поле. Рассмотрим модельный вариант.
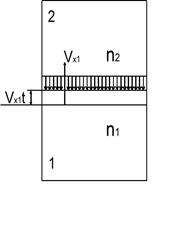 Пусть дан сосуд. В нем находится газ, который разделен на две части – 1 и 2, между которыми действует силовое поле.
Пусть дан сосуд. В нем находится газ, который разделен на две части – 1 и 2, между которыми действует силовое поле.
Допустим, что в начальный момент времени число молекул было одинаковым в обеих половинках. Объемы тоже одинаковы. Следовательно, концентрации также равны.
Однако, из-за действия силового поля количество молекул, переходящих из второй области в первую за единицу времени будет превышать число молекул, переходящих из первой области во вторую. В результате концентрация молекул в первой области будет возрастать, а во второй – убывать. В итоге число молекул, переходящих из области 2 в область 1 начнет снижаться, а обратный поток увеличится.
Таким образом, через определенный промежуток времени потоки выровняются, и концентрация в областях перестанет изменяться. В конечном итоге в первой области будет концентрация 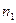 , во второй области -
, во второй области - 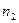 . В таком равновесном состоянии система будет находиться как угодно долго. Нашей задачей является установить связь между этими установившимися концентрациями.
. В таком равновесном состоянии система будет находиться как угодно долго. Нашей задачей является установить связь между этими установившимися концентрациями.
Выделим в первой области молекулу со скоростью 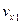 (ось направим вертикально вверх). Предполагается, что молекула находится недалеко от границы и через небольшой промежуток времени
(ось направим вертикально вверх). Предполагается, что молекула находится недалеко от границы и через небольшой промежуток времени 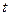 достигает её и переходит во вторую область. Выделим соответствующий объёмчик высотой
достигает её и переходит во вторую область. Выделим соответствующий объёмчик высотой 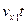 . Будем считать, что он цилиндрический с основанием
. Будем считать, что он цилиндрический с основанием 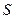 . Тогда
. Тогда
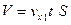 .
.
Число молекул попадающих в этот объем и имеющих проекции скорости 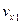 обозначим через
обозначим через 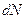 . Все они переходят во вторую область. Тогда
. Все они переходят во вторую область. Тогда
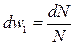 ,
,
где 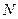 – число молекул в этом объеме,
– число молекул в этом объеме, 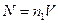 .
.
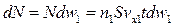 .
.
Пусть 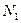 - число молекул, переходящих из первой области во вторую за некоторый достаточно малый промежуток времени
- число молекул, переходящих из первой области во вторую за некоторый достаточно малый промежуток времени 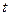
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
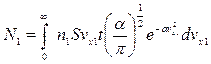 .
.
Проводя аналогичные рассуждения для молекул, переходящих из второй области в первую можно записать, что
 .
.
Так как система находится в состоянии равновесия, то 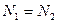 . Значит, эти интегралы можно приравнять
. Значит, эти интегралы можно приравнять
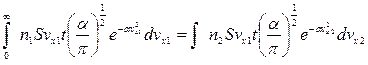 ,
,
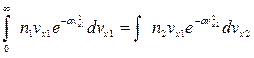 .
.
Обозначим потенциальную энергию, которую приобретает молекула при переходе из первой области во вторую через 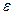 . Тогда можем записать, что
. Тогда можем записать, что
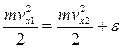 (2).
(2).
(Состояние равновесия не нарушится, если при переходе из первой области во вторую молекула 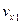 превращается в молекулу
превращается в молекулу 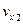 , и наоборот).
, и наоборот).
Возьмем дифференциалы от обеих частей выражения (2)
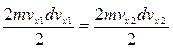 ,
,
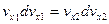 .
.
Сравним наши интегралы. Если 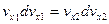 , то
, то 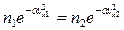 .
.
Выразим 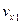 из (2)
из (2)
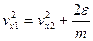 .
.
Тогда:
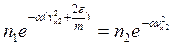 ,
,
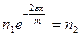 .
.
Подставляя выражение для 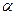 окончательно получим
окончательно получим
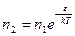 (3).
(3).
Полученное соотношение (3) называется законом распределения Больцмана.
В более общем смысле
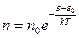 (3’),
(3’),
где 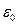 -потенциальная энергия, которая соответствует области
-потенциальная энергия, которая соответствует области 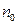 .
.
Воспользуемся формулой 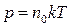 . Выразим
. Выразим 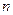 и подставим в (3’)
и подставим в (3’)
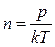 ,
,
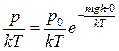 ,
,
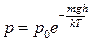 /
/
В виде следствия получили формулу, которая носит название барометрической.
|
|
