Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Факторною Х та результативною У ознаками

Y Х			…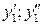
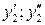
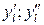
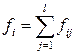
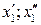
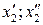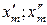
…	f 11 f 21 … fm 1	f 12 f 22 … fm 2	… … … …	f 1 l f 2 l … fml	f 1 f 2 … fm
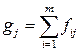
	g 1	g 2	…	gl	n

Позначення: 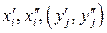– відповідно нижня та верхня межі і -го (j -го) інтервалу значень ознаки Х (Y), при цьому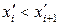 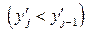; f_ij – число пар (х_е; у_е), для яких х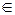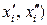_е [ і у_е 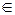[ 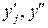_j); f_i (g_j) – число пар (х_е; у_е), для яких х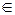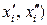_е [ (у_е [ )).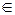

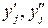При проведенні комбінаційного групування кількість m (l) інтервалів значень ознаки Х (Y) та їх ширина hx_i (hy_j) вибираються дослідником суб’єктивно або на основі, наприклад, рекомендацій, наведених у л. р. № 1 для побудови і. в. р.

При цьому бажано, щоб групи (або інтервали) були кількісно однорідними і m, l 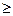3.

Вважатимемо групу кількісно однорідною, якщо розподіл ознаки всередині відповідного інтервалу близький до рівномірного.

Очевидно, що 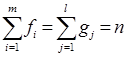– обсяг сукупності.

Маючи таблицю 3.1. можна провести попередній аналіз взаємозалежності між Х та Y за таким очевидним правилом:

– якщо частоти f_ij, розташовані приблизно на головній діагоналі таблиці (тобто між її лівим верхнім та правим нижнім кутами), суттєво більші за інші або ці інші частоти, в основному, дорівнюють нулю, то є підстави припустити наявність прямого зв’язку між фактором Х та результатом Y;

– якщо вищенаведені співвідношення між f_ij мають місце для побічної діагоналі таблиці, то можна припустити наявність зворотного зв’язку між Х та Y;

– якщо всі частоти f_ij розподіляються приблизно рівномірно по всіх клітинках таблиці, то логічно припустити, що зв’язок між Х та Y відсутній.

В інших випадках, тобто, коли частоти f_ij суттєво відрізняються одна від одної, але візуальний їх аналіз не дає можливості висунути певне припущення про наявність або напрям зв’язку, виникає необхідність формалізації перевірки можливої залежності між ознаками.

Формально перевірку істотності (тобто, існування) зв’язку можна виконати за допомогою критерія Пірсона 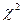, спостережене значення якого обчислюється за даними таблиці 3.1 за формулою:

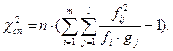
За таблицею критичних точок критерія 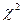(див. додаток 6) знаходимо критичне його значення 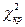в залежності від рівня значущості 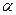і числа степенів вільності 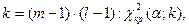після чого перевірка здійснюється за правилом: якщо 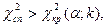то вважаємо зв'язок істотним (тобто, існуючим) з надійністю 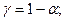якщо 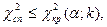то зв'язок вважається відсутнім з тією ж надійністю. Величина 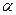являє собою імовірність ризику зробити помилку, оцінивши зв'язок як істотний при фактичній його відсутності. На практиці число 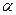вибирають не більшим за 0, 1.

Якщо перевірка за критерієм Пірсона 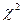підтвердила істотність зв’язку, то його щільність можна оцінити за допомогою коефіцієнта спряженості Крамера, який обчислюється за формулою:

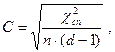
де 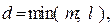n − обсяг сукупності. Величина С може набувати значень від 0 до 1: .

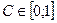При цьому щільність зв’язку оцінюється за правилом: чим ближче значення С до1 (0), тим зв'язок більш (менш) щільний.

При бажанні вимірювання щільності залежності можна формалізувати, керуючись правилом трисекції: залежністьбудемо вважати

– щільною (або тісною), якщо ;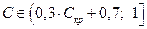

– помірною (або середньою), якщо ;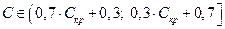

– слабкою (або незначною), якщо ,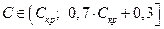

де

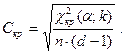
Висновки, зроблені за результатами застосування вищенаведеного правила слід вважати вірними з тією ж надійністю 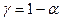.