Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Основні поняття. Основною формою зв’язків між реальними явищами і процесами є причинно-наслідкова залежність

Основною формою зв’язків між реальними явищами і процесами є причинно-наслідкова залежність. У статистиці причини зазвичай називають факторами, а ознаки, що їх характеризують – факторними ознаками (Х); наслідки називають результатами, а ознаки, що їх характеризують – результативними ознаками (Y).

Усі можливі види зв’язків можна розділити на групи за двома основними ознаками:

а) за числом факторів – однофакторні і багатофакторні;

б) за статистичною природою – функціональні і стохастичні (або випадкові).

При функціональній залежності кожному можливому значенню х факторної ознаки Х відповідає певне єдине значення у результативної ознаки Y.

При стохастичній залежності кожному можливому х відповідає певна множина значень у, тобто, для фіксованого Х значення Y можуть варіювати, утворюючи ряд розподілу ознаки Y, який називається умовним, оскільки він утворений за умови, що ознака Х прийняла певне значення. Таким чином, стохастичний зв’язок між ознаками проявляється у зміні умовних розподілів результату Y при зміні значення фактора Х.

Різновидом стохастичного зв’язку є кореляційний зв’язок, коли зі зміною значень х фактора Х змінюються середні значення 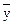відповідного умовного розподілу ознаки Y.

Очевидно, що кореляційний зв’язок можна розглядати як окремий випадок стохастичного зв’язку, оскільки можлива ситуація, коли зі зміною значень х умовний розподіл ознаки Y змінюється (тобто, стохастичний зв’язок існує), а середні значення 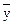для всіх умовних розподілів не змінюються (тобто, кореляційний зв’язок не існує).

Далі будемо розглядати і вивчати однофакторну стохастичну кореляційну залежність між ознаками. При цьому метою повного дослідження залежності Y від Х є: а) встановлення факту істотності (тобто існування) або неістотності (тобто неіснування) цієї залежності; б) вимірювання щільності (тобто тісноти) зв’язку; в) встановлення напряму зв’язку, який є прямим (зворотним), якщо зі збільшенням значень фактора Х значення результату Y зростають (спадають); г) виявлення виду та характеру зв’язку, що визначається функцією 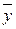= f(x), якою можна апроксимувати залежність середніх значень 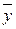результату Y від значень х фактора Х. При цьому вид залежності визначається видом функції (наприклад, лінійна, квадратична), а характер залежності – характером зміни цієї функції зі зростанням її аргументу х, який може бути рівномірним, прискореним або уповільненим.

Функція 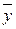= f(x), яка пов’язує значення х факторної ознаки і середні значення 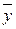відповідного умовного розподілу результативної ознаки, називається лінією регресії. Вона є головною характеристикою кореляційної залежності в тому розумінні, що, маючи цю функцію, можна провести повне дослідження залежності Y від Х, тобто реалізувати вищенаведені п. п. а) – г).

Лінія регресії, як і будь-яка функція, може задаватись таблично, аналітично і графічно.

Як правило, графічне зображення лінії регресії має другорядне, в основному, ілюстративне значення.

На табличному й аналітичному способах задання лінії регресії ґрунтуються два основних методи вивчення кореляційної залежності: відповідно, метод аналітичного групування та метод кореляційно-регресійного аналізу.