
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Інтервальні оцінки для генеральних середньої та частки
|
|
Інтервальною оцінкою ( або надійним, або довірчим інтервалом) параметра  генеральної сукупності називається такий інтервал
генеральної сукупності називається такий інтервал 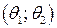 , який із заданою надійністю ( або надійною, або довірчою імовірністю) γ накриває параметр
, який із заданою надійністю ( або надійною, або довірчою імовірністю) γ накриває параметр  , що оцінюється. При цьому
, що оцінюється. При цьому 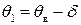 ,
, 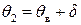 , де
, де 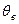 – точкова оцінка (або вибіркове значення) параметра
– точкова оцінка (або вибіркове значення) параметра  , величина δ знаходиться за нижченаведеними формулами і визначає точність інтервальної оцінки: чим менше δ, тим вища точність.
, величина δ знаходиться за нижченаведеними формулами і визначає точність інтервальної оцінки: чим менше δ, тим вища точність.
У статистиці величина δ називається граничною помилкою і обчислюється за формулою:
δ =t* μ,
де величина t називається довірчим числом (або коефіцієнтом довіри), а μ – середньою (або стандартною) помилкою.
Довірче число t=tγ (n) знаходиться за таблицями критичних точок розподілу Стьюдента для двосторонньої критичної області в залежності від надійності γ і обсягу вибірки п (див. додаток 3, число степенів вільності k=n– 1, рівень значущості α = 1 –γ). Так, наприклад, t 0, 95(10)=2, 26.
Якщо п > 30, то прийнято вважати, що розподіл Стьюдента з достатньою для практичних потреб точністю співпадає з нормальним розподілом і тоді число t=tγ можна знаходити за таблицями значень інтегральної функції Лапласа Ф(х) (див. додаток 5) із умови: Ф(tγ ) =γ / 2. Так, наприклад, t 0, 95=1, 96. Крім того, число tγ можна знаходити за таблицею додатку 3, поклавши 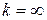 .
.
Середні помилки μ для інтервальних оцінок генеральної середньої 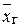 та генеральної частки р знаходяться за формулами, наведеними в таблиці 2.1:
та генеральної частки р знаходяться за формулами, наведеними в таблиці 2.1:
Таблиця 2.1
Середні помилки інтервальних оцінок параметрів 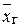 та р
та р
| Схема відбору | для 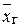 (п > 30) (п > 30)
| для 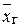 ( (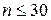 ) )
| для р |
| Повторна | 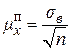
| 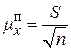
| 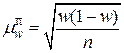
|
| Безповторна | 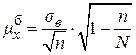
| 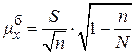
| 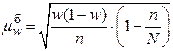
|
Позначення: 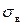 – вибіркове середнє квадратичне відхилення, яке обчислюється за формулою (1.7), наведеною в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.;
– вибіркове середнє квадратичне відхилення, яке обчислюється за формулою (1.7), наведеною в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.; 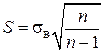 – виправлене середнє квадратичне відхилення;
– виправлене середнє квадратичне відхилення; 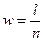 – вибіркова частка варіант, що задовольняють задану умову; l – число варіант, що задовольняють задану умову; N – обсяг генеральної сукупності.
– вибіркова частка варіант, що задовольняють задану умову; l – число варіант, що задовольняють задану умову; N – обсяг генеральної сукупності.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Точковими оцінками генеральних середньої 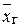 та частки р є відповідно вибіркові середня
та частки р є відповідно вибіркові середня 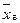 та частка w; при цьому
та частка w; при цьому 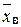 обчислюється за формулами (1.1) – (1.3), наведеними в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.
обчислюється за формулами (1.1) – (1.3), наведеними в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.
Таким чином, надійні інтервали для генеральних середньої та частки мають такий вид:
– для повторної вибірки:
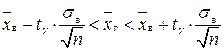 , якщо п > 30; (2.1)
, якщо п > 30; (2.1)

 , якщо п ≤ 30; (2.2)
, якщо п ≤ 30; (2.2)
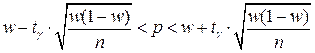 . (2.3)
. (2.3)
– для безповторної вибірки:
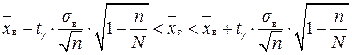 , якщо п > 30; (2.4)
, якщо п > 30; (2.4)
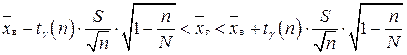 , якщо п ≤ 30; (2.5)
, якщо п ≤ 30; (2.5)
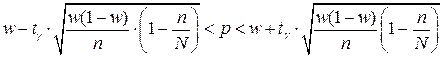 . (2.6)
. (2.6)
Очевидно, якщо обсяг вибірки п набагато менший за обсяг генеральної сукупності N (n< < N), то n/N ≈ 0 і формули (2.1) – (2.3) майже збігаються з формулами (2.4) – (2.6). Тому у статистичній практиці прийнято вважати, що якщо n/N < 0, 05, то надійні інтервали можна знаходити за більш простими формулами (2.1) – (2.3) незалежно від схеми відбору.
Слід зауважити, що формули для μ х та μ w виведено в припущенні відповідно нормального та біноміального розподілів генеральної сукупності, проте на практиці вони використовуються незалежно від виду розподілу останньої.
|
|
