
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Реализация в МКЭ
|
|
Ползучесть материала характеризуется с помощью констант материала С1...С12. Для неклассических моделей может использоваться большее число констант.
Расчет ползучести в МКЭ может производится явным и неявным методом (в данном случае термины «явный» и «неявный» относятся лишь к ползучести, но не методу численного интегрирования задачи вообще).
Неявный метод более устойчив, быстр, точен и рекомендуется для использования по умолчанию. Он подходит для задач с большими деформациями ползучести и просто с большими деформациями, так же как и для задач, учитывающих влияние температуры.
Явный метод используется для анализа очень малых промежутков времени или переходных процессов (далее не рассматривается).
Приведенные полные деформации на очередном шаге интегрирования определяются как:
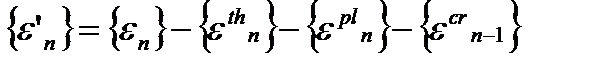 . (4.42)
. (4.42)
Данное выражение (4.42) по смыслу аналогично выражению (4.14), которое использовалось для пластичности.
Эквивалентные приведенные деформации определяются следующим образом:
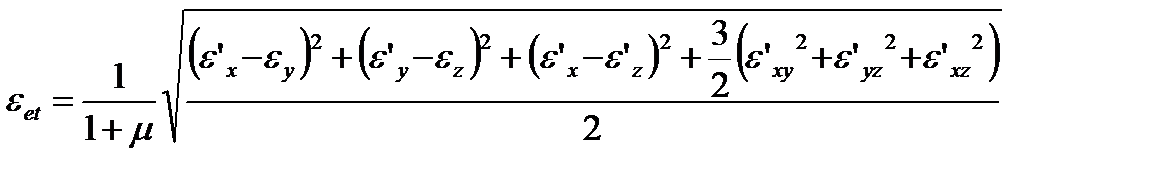 , (4.43)
, (4.43)
а эквивалентные напряжения определяются как:
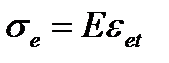 . (4.44)
. (4.44)
Эквивалентное приращение деформаций ползучести Δ ε cr обычно предполагается положительным (при постоянной нагрузки деформации как правило не уменьшаются). Величина приращения деформаций ползучести может быть определена как скорость деформаций ползучести, умноженная на шаг по времени:
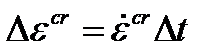 . (4.44)
. (4.44)
Соотношения, определяющие скорость деформаций ползучести для некоторых моделей ползучести приведены в таблице 4.1. При этом в таблице 4.1 приняты следующие обозначения:
T – температура в градусах Кельвина;
t – время в конце шага интегрирования;
С1...С12 – константы материала определяемые для каждой модели (в разных моделях одинаковыми символами могут обозначаться разные по физическому смыслу константы).
Поскольку получение всех констант С1...С12 для конкретного материала может представлять трудность, а поведение материала не всегда соответствует указанным ниже моделям, в пакетах МКЭ обычно предусмотрена возможность задавать пользовательские модели ползучести.
Таблица 4.1 - Скорость деформаций ползучести
| Модель ползучести | Соотношения |
| Упрочнение по деформациям | 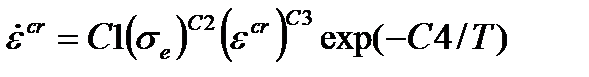
|
| Упрочнение по времени | 
|
| Обобщенная экспоненциальная | 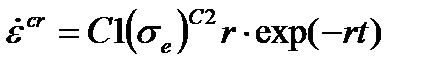 , , 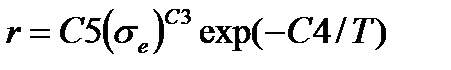
|
| Обобщенная Грэма | 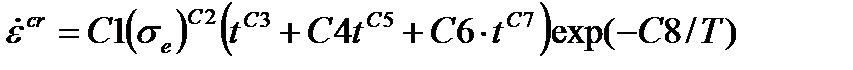
|
| Обобщенная Блекбурна | 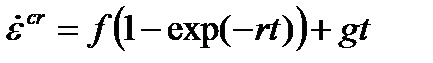 , ,
 , , 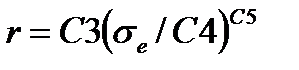 , , 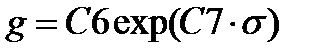
|
| Приведенное упрочнение по времени | 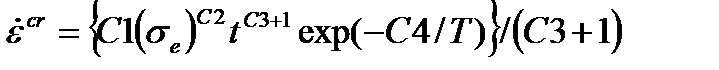
|
| Приведенное упрочение по деформациям | 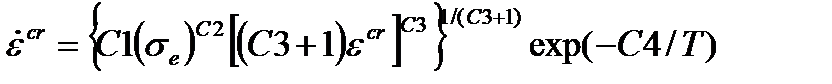
|
| Обобщенная Горофало | 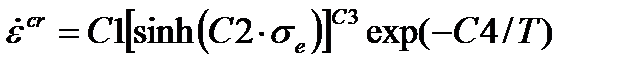
|
| Экспоненциальная | 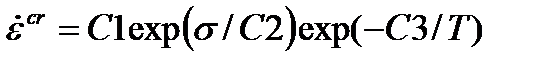
|
| Нортона | 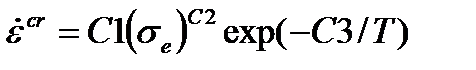
|
| Упрочнение по времени | 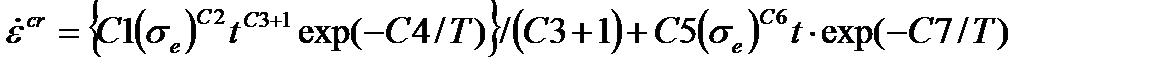
|
| Рациональный многочлен | 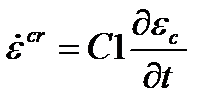 , , 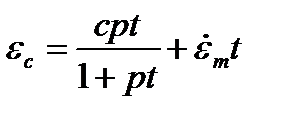 , ,  , , 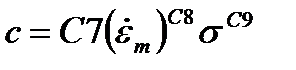 , , 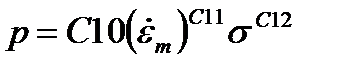
|
| Обобщенное упрочнение По времени | 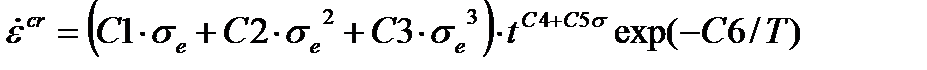
|
Коэффициент ползучести (мера приращения деформаций ползучести) в точке интегрирования вычисляется как:
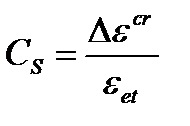 . (4.45)
. (4.45)
Приращение деформаций ползучести на n -м шаге интегрирования определяется по компонентам тензора деформаций:
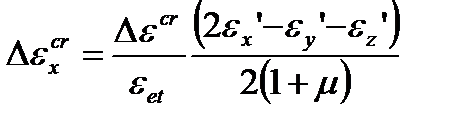 , (4.46)
, (4.46)
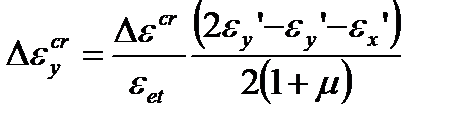 , (4.47)
, (4.47)
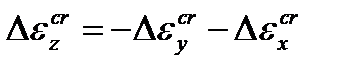 , (4.48)
, (4.48)
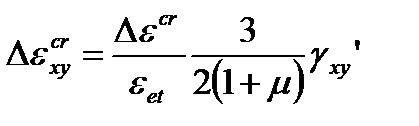 , (4.49)
, (4.49)
 , (4.50)
, (4.50)
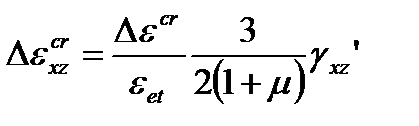 . (4.51)
. (4.51)
Заметим, что компоненты приведенных полных деформаций могут иметь значения от -1 до +1.
Формулы для расчета упругих деформаций и полных деформаций ползучести на n -м шаге интегрирования приведены ниже (только для х-компонента):
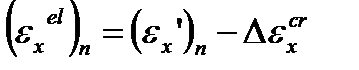 , (4.52)
, (4.52)
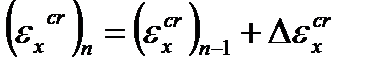 . (4.53)
. (4.53)
Напряжения рассчитываются на базе компонентов (ε ')n, это дает корректные значения напряжений для задач с фиксированными нагрузками (ползучесть) и максимальные напряжения за каждый шаг интегрирования для задач с фиксированными перемещениями (релаксация).
Отдельно отметим, что шаг интегрирования Δ tn рекомендуется выбирать исходя из условия, чтобы максимальное значение коэффициента ползучести CMAX не превышало 0, 1. В любом случае при CMAX превышающем 0, 25 обычно расчет останавливается.
|
|