Билиненйая и мультилинейная модели с изотропным (механическим) упрочнением

Эти модели используют критерий текучести по фон Мизесу, ассоциированный закон текучести и изотропное (механическое) упрочнение.

Эквивалентные напряжения (4.4) записываются как:

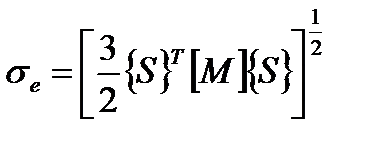, (4.18)

где { S } – девиаторные напряжения, ,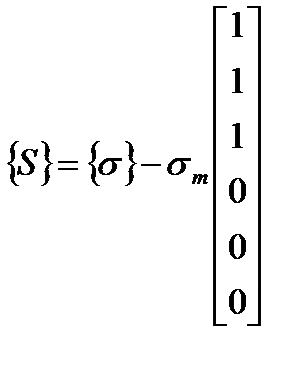

в котором ­ σ _m - величина гидростатического давления, равная:

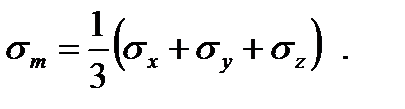
Заметим, что формула (4.17) эквивалентна (2.79) и получается из неё с помощью элементарных преобразований.

В случае, если эквивалентные напряжения σ _e равны текущему значению предела текучести σ _k, критерий текучести можно записать в следующем виде:

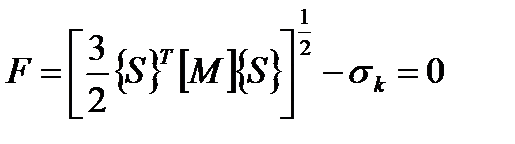. (4.19)

Для механического упрочнения текущее значение предела текучести σ _k является функцией от величины совершенной пластической работы. В случае изотропной пластичности (о которой сейчас и идёт речь) σ _k может быть определен через эквивалентные пластические деформации (4.17) и графика напряжений-деформаций (рисунок 4.4).

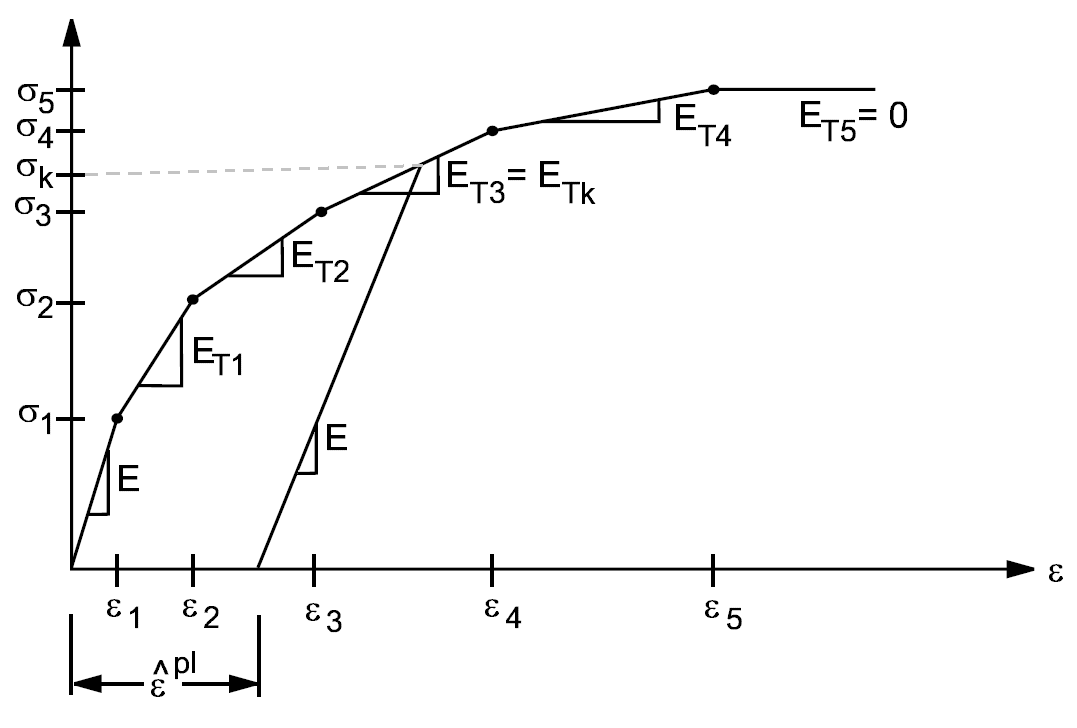
Рисунок 4.4 - Определение текущего значения предела текучести σ _k

(Билиненйая и мультилинейная модели с изотропным (механическим) упрочнением)