Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обчислення середнього арифметичного числа колосків у колосі пшениці
|
|
| Кількість колосків у колосі (х) | Число колосів (частоти f) | fх | х-М | (х-М)2 | (х-М)2 f |
| -2, 44 -1, 44 -0, 44 0, 56 1, 56 2, 56 | 5, 95 2, 07 0, 19 0, 31 2, 43 6, 55 | 47, 6 35, 19 4, 94 8, 68 34, 02 45, 85 | |||
| 176, 28 | |||||
| n=∑ f = 100 |
= 
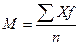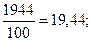М=19, 44 колоска
Таким чином, середнє арифметичне дорівнює 19, 4 колоска. Ця величина найбільше характерна для даної вибірки рослин.
Обчислення стандартного відхилення. Середнє арифметичне не відбиває ступеня мінливості ознаки в даної групи особин, сорту і т.д. Для характеристики мінливості використовують стандартне (середнє квадратичне) відхилення. Воно позначається літерою d; це число виражається в тих же одиницях, що і середня арифметична. Стандартне відхилення обчислюють по формулі:
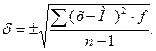
У нашому прикладі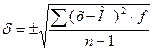 
= 
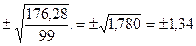колоска.
Це означає, що кожний колос у середньому відрізняється від середньої арифметичної М на 1, 34 колоска.
Стандартне відхилення іноді називають помилкою окремого варіанта, тому що, знаючи значення М і d для даного варіаційного ряду, можна визначити, чи відноситься дана особина до цього ряду. Вона може відноситися до даного ряду, якщо її відхилення від середньої арифметичної не перевищує 3 d. У аналізованому прикладі М = 19, 4, d = 1, 34, найбільше значення варіанта дорівнює 22, найменше—17. Відхилення складе: 22-19, 4 =+2, 6; 17-19, 4=-2, 4.
Так як відхилення найбільшого і найменшого варіантів від середньої арифметичної не перевищують 3 d, тобто 4, 02, то усі особини відносяться до даного варіаційного ряду. Отже, межі модифікаційної мінливості визначаються М±3 d .
Обчислення коефіцієнта варіації. Для порівняння варіювання ознак різної розмірності, наприклад, кількість зерен у колосі і довжина стебла рослин або мінливості однієї і тієї самої ознаки в різних сортів, а також, щоб мати можливість судити про ступінь вирівняності досліджуваного матеріалу, обчислюють коефіцієнт варіації (V). Роблять це за формулою:
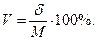
У нашому прикладі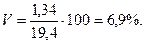 
Мінливість варіюючої ознаки у цьому випадку незначна, тому що коефіцієнт варіації менше 10%. Прийнято вважати мінливість середньою, якщо коефіцієнт варіації перевищує 10%, але нижче за 20%, і великою, якщо коефіцієнт варіації вищий за 20%.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Щоб порівняти розмах мінливості різноманітних ознак у рослин того самого сорту, варто обчислити стандартне відхилення (d) і коефіцієнт варіації (V) для цих ознак. Наприклад, для трьох ознак рослин пшениці М, d і V мають такі значення:
| Ознаки | М | d | V% |
| Вага зернівок з однієї рослини (г) | 3, 2 | 1, 4 | 43, 8 |
| Кількість зернівок у головному колосі | 8, 0 | 19, 5 | |
| Кількість колосків у головному колосі | 19, 4 | 1, 34 | 6, 9 |
Найменше варіює число колосків у головному колосі (V=6, 9%). Найбільш мінлива ознака — вага зернівок з однієї рослини (V=43, 8%). Отже, число колосків у колосі мало змінюється під впливом зовнішніх умов; вага ж зернівок з рослини і кількість насінин у головному колосі в більшій мірі залежать від умов зростання і схильні до значної мінливості.
Обчислення похибки середньої арифметичної. Похибка середньої арифметичної позначається m. Вона показує, якої припустилися похибки, вважаючи, що середня арифметична вибірки дорівнює середній арифметичній генеральної сукупності.
Похибку середньої арифметичної обчислюють за формулою:
У нашому прикладі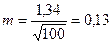 
колоска, тобто похибка середньої арифметичної дорівнює ±0, 13 колоска.
Після обчислення m можемо сказати, що сорт пшениці, що вивчався нами, має середнє число колосків 19, 4±0, 13.
Якщо виходити з того, що розмах мінливості середніх арифметичних вибірок підпорядковується правилу трьох d, то аналізований сорт має середнє число колосків у колосі 19, 4 ± 3´ 0, 13 колоска, тобто від 19, 0 до 19, 8 колоска.
Дані, отримані в результаті статистичного вивчення тих або інших ознак заносять у таблицю (табл. 9).
Таблиця 9
|
|