Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Оптическая разность хода.

Для получения когерентных световых волн применяют метод разделения волны на 2 части, которые после прохождения разных оптических путей накладываются друг на друга и наблюдается интерференционная картина.

Рис.

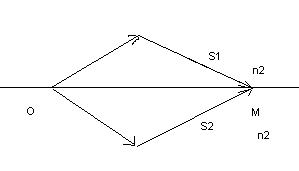
Пусть разделение волны на две когерентные происходит в точке О до точки М, первая волна проходит путь S1, а вторая путь S2. Если в точке О фаза колебания равна wt, то в точке М получим:

E₁ = A₁cosw(t- )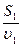

E₂ = A₂cos w(t- 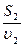), где ; ;

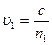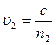Тогда разность фаз в точке М будет:

δ =w(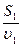 - 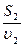)=2π ν ( 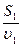- 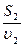)=2π ν ( - )= ( - )= ( - ) =>

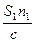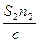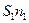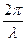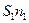δ = 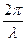Δ: Δ = 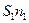- ; Δ =L₁-L₂

произведение геометрической длины пути световой волны в данной среде на показатель преломления этой среды называется оптической длиной пути L.

Δ – оптическая разность хода.

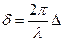
Δ = S₁n₁ – S₂n₂ = l₁ – l₂

Если оптическая разность хода равна целому числу произведения геометрической пути световой волны в данной среде и колебания точки M будут происходить в одинаковой фазе.

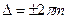, m = 0, 1, 2… =>

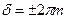, т.е Δ – не что иное как условие интерференционного max.

Если 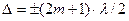, то 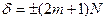Колебания в точке M будут в противофазе, если их оптическая разность хода равна нечетному числу длин полуволн – условие интерференционного min.