Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема: Побудова моделі для дослідження конфліктної ситуації з використання принципу оптимальності Парето.

Множина учасників конфліктної ситуації

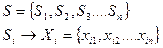
х – стратегія

і – номер учасника

1, 2, 3… - номер стратегії

Під стратегією учасника конфліктної ситуації будемо розуміти будь-яку можливу дію цього учасника, в рамках досліджуваної ситуації, не залежно від імовірності її здійснення.

Всі стратегії всіх учасників оцінюються з точки зору кожного учасника експертами і результати оцінки подаються у вигляді таблиці:

S/x	S1	S2	…..	Sn
X 11	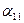Оцінка з точки зору першого учасника стосовно його першої стратегії	Оцінка з точки зору другого учасника стосовно першої стратегії першого
X12
X13
X21	Оцінка з точки зору першого учасника стосовно першої стратегії другого ігрока	Оцінка з точки зору другого учасника стосовно його першої стратегії
X22
X23
…..
Xn1
Хnk

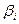
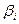- ваговий коефіцієнт, що визначає рівень впливу кожного учасника на конфліктну ситуацію. Діапазон від 0 до 1, і робимо припущення, що сума всіх цих коефіцієнтів 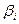= 1. тобто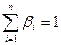

Терба створити відповідну шкалу, для оцінки значимості стратегії, формулюємо твердження стосовно мінімальної та максимальної оцінки.

Будь-який можливий варіант майбутнього розвитку досліджуваної ситуації буде належати до множини усіх можливих реалізацій, яка є декартовим добутком множини можливих стратегій усіх учасників.

Декартовий добуток:

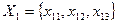
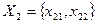
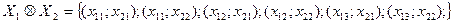
Розв’язок конфліктної ситуації буде належати цій множині (множині можливих реалізацій)

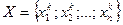- загальний вид розвязку, який буде містити по одній стратегії кожного учасника, який буде оптимальним рішенням для всіх.

Результати декартового добутку() записуються в таблицю:

Х S1 S2 …. Sn

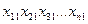
	f11	f21		fn1
…..

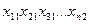
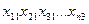
f – цільова функція, яка оцінює з точки зору кожного учасника набір реалізацій.

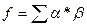
Чим більше є значення цільовох функції для конкретної реалізації з точки зору певного учасника, тим більшою мірою в цьому варіанті розвитку конфліктної ситуації враховано інтереси цього учасника, при розгляду власних стратегій у комбінації зі стратегіями інших учасників завжди існує варіант для кожного з учасників, який характеризується своєю найкращою стратегією і найгіршими з точки зору даного учасника іншими стратегіями. Значення цільової функції f, яке відповідає такому варіанту називається мінімально гарантованим результатом

Порівнює всі реалізації з мінімально гарантованою і ті, які мають цільову функцію менше – відкидаємо. Все реалізації, що залишились утворюють множину раціональних рішень. А серед неї відбувається відбір оптимального за Парето. Оптимальність за Парето – це такий стан системи, за якого значення кожного часного показника не може бути покращено без погіршення інших. Вона може не існувати, може існувати одна або множина.

Пример:

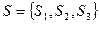
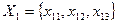
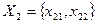
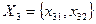
S1 – Росія

S2 - Україна

S3 - ЄС

S1:

х11 – Росія перекриє газ

х12 – зростання ціни на газ

х13 – збільшення ціни за транзит

S2:

х21 – альтернативні джерела

х22 – закупка німецького газу

S3:

х31 – нейтральная позиция

х32 – підтримка України

Шкала:

1 – найгірший варіат

2 – середній

3 - максимальний

S/x	S1	S2	S3
х 11
х12
х13
х21
х22
х31
х32
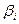
	0, 5	0, 3	0, 2

S/x	S1 (2)	S2 (1, 8)	S3 (1, 7)
	2*0, 5+1*0, 3+1*0, 2 = 1, 5	2*0, 5+3*0, 3+3*0, 2 = 2, 5	2, 2
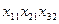
	1, 7	2, 3
	1, 5	2, 2	2, 5
	1, 7		2, 7
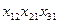
	3*0, 5+1*0, 3+1*0, 2 = 2		2, 2
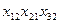
	2, 2	1, 8
		1, 7	2, 5
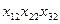
	2, 2	1, 5	2, 3
	1, 5
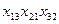
	1, 7	2, 8
	1, 5	2, 7
	1, 7	2, 5

S1 = 3*0, 5+1*0, 3+1*0, 2 = 2 (для першого гравця з першоъ таблицы беромо найбыльшу цифру серед її стратегій, та найменші серед інших стратегій)

S2 = 1, 8

S3 = 1, 7