Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Метод начальных параметров

Метод начальных параметров основан на дополнении поставленных для краевой задачи граничных условий в начале участка интегрирования некоторыми параметрами, называемыми начальными. Эти параметры выбирают так, чтобы полученная при этом совокупность начальных условий полностью определяла решение поставленной задачи.

Пусть дана краевая задача для системы n линейных дифференциальных уравнений первого порядка.

(12)

с граничными условиями на концах интервала [0, l ]

;

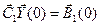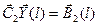(13)

где 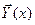– вектор неизвестных у1(х), y2(х),..., уn(х);

А(х) – матрица коэффициентов при неизвестных;

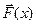– вектор свободных членов;

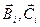– векторы постоянных интегрирования.

Общий интеграл системы уравнений (3.40) запишем в следующем виде:

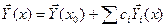(14)

где 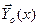– частное решение матричного уравнения (12), удовлетворяющее всем нулевым начальным условиям ;

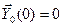– частное решение соответствующего уравнению (12) однородного уравнения 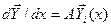, удовлетворяющее начальным условиям 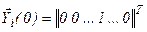, где все элементы равны нулю, кроме i -гo, который равен единице; ci – постоянные интегрирования.

Подстановкой полученного по (12) решения в условия (13) получают систему n алгебраических уравнений для определения ci. Найденные постоянные подставляют в (14), откуда находят решение исходной краевой задачи.