Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Пример 8а.

> with(plots):

> inequal({ y-x< =0, 2*y-x> 0, y> =2, y< 3}, x=0..8, y=1..4, optionsfeasible=(color=red),

optionsopen=(color=blue, thickness=2, linestyle=3),

optionsclosed=(color=green, thickness=3),

optionsexcluded=(color=yellow));

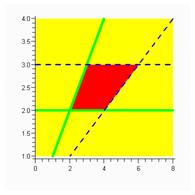
ЗАДАНИЕ 8. Нарисуйте область, ограниченную прямыми: у=3х, у=х/2, у=1, у=-х+8. Правые границы сделайте пунктирными. Для оптимального выбора масштаба сначала нарисуйте все линии на одном графике с помощью команды plot.

К сожалению, команда inequal() действует только для линий, заданных линейными уравнениями. Для нелинейных уравнений области можно получить, нарисовав все линии на одном графике с помощью команды plot.

ЗАДАНИЕ 9. Получите область, ограниченную прямыми (выберите свой вариант). Если прямые заданы равенствами, задайте область с помощью соответствующих неравенств.

1.	2.	3.	4.
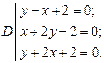
5.	6.	7.	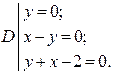8.
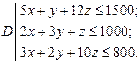
9.	10.	11.	12.
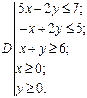
13.	14.	15.	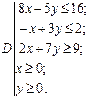16.
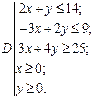
17.	18.	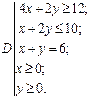19.	20.
21.

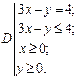
10. Команда polygonplot() строит на плоскости один или несколько многоугольников, заданных своими вершинами. Каждый многоугольник задается в виде списка координат его вершин, представленных в форме двухэлементных списков. В случае отображения нескольких многоугольников они задаются либо списком, либо множеством.