Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Двумерные команды пакета plots

5. На плоскости кроме прямоугольной декартовой системы координат используются и другие. Одной из наиболее часто применяемой является полярная система координат, в которой положение точки задается также двумя величинами. Они представляют собой длину r радиус-вектора, проведенного из начала координат в заданную точку, и угол наклона j этого вектора относительно положительного направления горизонтальной оси координат. Многие " замечательные" плоские кривые легче и проще задавать именно в полярной системе координат. Например, окружность радиуса a с центром в начале координат в полярной системе координат задается простым уравнением r = a, тогда как в декартовой системе координат эта же окружность задается уравнением в неявном виде .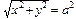

Для отображения графика функции, заданной в полярной системе координат, в пакете plots существует функция polarplot(). Ее синтаксис похож на синтаксис команды plot() за одним исключением – не задается третий параметр, ограничивающий диапазон изменения значений, в данном случае длины радиус-вектора:

polarplot(r, phi=диапазон, опции);

Параметр r – это выражение или функция, зависящие от независимой переменной phi, интерпретируемой как угол поворота радиус-вектора относительно горизонтальной оси. Диапазон изменения независимой переменной может отсутствовать, тогда используется диапазон изменения по умолчанию -Pi..Pi. остальные параметры представляют собой такие же опции, что и в функции plot(). Использование команды построения окружности в полярной системе координат демонстрируется в примере 5.