Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вычисление суммы членов ряда

Вычисление суммы членов ряда рассмотрим на примере тригонометрической функции . Известно, что данная функция может быть представлена разложением в следующий ряд:

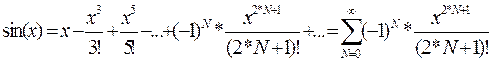, (22)

где 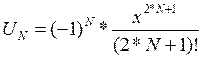- общий член ряда.

Очевидно, сумма членов ряда S может быть вычислена только при конечном (заданном) числе членов ряда, предположим NZ = 10, или условием окончания вычислений может быть неравенство вида , где достаточно малая величина, предположим или 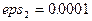. (Известно, что в сходящихся рядах , т.e. значение модуля каждого последующего члена ряда меньше предыдущего).

Приведем рекуррентную формулу для вычисления значения текущего члена ряда:

, где 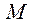- рекуррентный множитель. (23)

Для нашего примера (уравнение 22)

M= 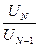= 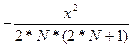. (24)

Покажем схему алгоритма вычисления суммы членов ряда на рис. 25.

Рис.25

СОДЕРЖАНИЕ

введение..................... Ошибка! Закладка не определена.

АЛГОРИТМИЗАЦИЯ..... Ошибка! Закладка не определена.

1. ВЫЧИСЛЕНИЕ СУММЫ (СУММИРОВАНИЕ) ЭЛЕМЕНТОВ ВЕКТОРА 6

2. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ ЭЛЕМЕНТОВ ВЕКТОРА........... 7

3. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ.................... 10

4. СУММИРОВАНИЕ (ВЫЧИТАНИЕ) МАТРИЦ................................. 12

5. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ МАТРИЦ.................................... 13

6. ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЯ МАТРИЦЫ НА ВЕКТОР.......... 14

7. ВЫЧИСЛЕНИЕ ЕДИНИЧНОЙ МАТРИЦЫ....................................... 14

8. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ................................................. 15

9. ИНВЕРТИРОВАНИЕ ЭЛЕМЕНТОВ ВЕКТОРА................................ 16

10. АЛГОРИТМ ПОИСКА МАКСИМАЛЬНОГО (ИЛИ МИНИМАЛЬ-НОГО) ЭЛЕМЕНТА ВЕКТОРА...................................................................... 17

11. АЛГОРИТМ СОРТИРОВКИ (УПОРЯДОЧИВАНИЯ) ЭЛЕМЕНТОВ ВЕКТОРА ИЛИ МАТРИЦЫ.......................................................................................... 18

12. ВЫЧИСЛЕНИЕ ПОЛИНОМА ПО СХЕМЕ ГОРНЕРА.................... 20

13. ВЫЧИСЛЕНИЕ СУММЫ ЧЛЕНОВ РЯДА Ошибка! Закладка не определена.