Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 6
|
|
Дана матрица A = { 
}, i, j=1, 2,..., N.
Необходимо вычислить элементы вектора X = { 
}, i = 1, 2,..., N. Каждый элемент вектора вычисляется как произведение i-го столбца и главной диагонали матрицы A.
Например, пусть N = 3 и известны все элементы матрицы A
A =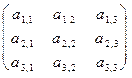 
= 
.
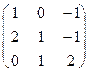Попутно отметим, что i-ая строка, j-ый столбец, главная и побочная диагонали матрицы A по сути является вектором.
Действительно,
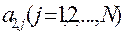- 2-ая строка (вектор),
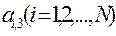- 3-ий столбец (вектор),
{ 
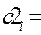}N - главная диагональ (вектор),
{ 
}N - побочная диагональ (вектор).
В соответствии с условием задачи (пример 6), элементы вектора xi могут быть рассчитаны следующим образом:
для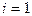 
= 
* + 
* 
+ 
* 
= 
;
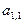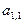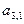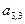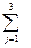
для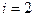 
= 
;
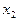для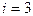 
.
Формализация данной задачи приводит к следующему выражению:
, i = 1, 2,..., N (8)
Два варианта разработки алгоритма данной задачи показаны на рис. 13.
Рис.13
|
|