Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Алгоритм сортировки (упорядочивания) элементов вектора или матрицы

Сортировка означает перестановку элементов вектора или матрицы в определенном порядке (по возрастанию или по убыванию) в соответствии с их значениями.

Рассмотрим алгоритм сортировки (упорядочивания) элементов вектора, когда значение каждого последующего элемента вектора больше предыдущего. Например, пусть исходный вектор X ={ }₆=(3, 4, 2, -1, 6, 0), тогда в результате сортировки получим вектор X =(-1, 0, 2, 3, 4, 6).

Существуют различные способы решения данной задачи. Рассмотрим один из них.

Процедура сортировки элементов вектора X по возрастанию их значенийследующая.

Первый шаг

Среди N-1 элементов вектора X (за исключением ) произведем поиск минимального элемента вектора 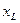и поменяем его местами с первым элементом, если значение 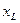< . В результате выполнения первого шага сортировки получим следующий вектор X =(-1, 4, 2, 3, 6, 0).

Второй шаг

Среди N-2 элементов вектора X (за исключением , 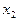) произведем поиск минимального элемента вектора 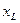и поменяем его местами со вторым элементом, если значение < 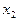. В результате выполнения второго шага сортировки получим вектор X =(-1, 0, 2, 3, 6, 4).

Очевидно, после выполнения N-1 шага (в нашем примере после 5 шагов) получим окончательный упорядоченный вектор X =(-1, 0, 2, 3, 4, 6).

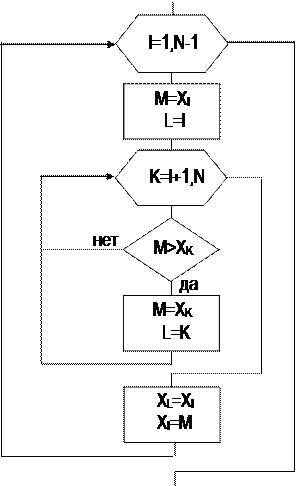
Алгоритм упорядочивания по возрастанию элементов вектора показан на рис. 22. Данный алгоритм пригоден для упорядочивания элементов вектора по убыванию с очевидной заменой знака " > " на знак " < " в блоке проверки условия (рис. 22).

Рассмотрим алгоритм сортировки элементов матрицы.

Дана матрица A ={ }_P*N . Необходимо упорядочить элементы столбцов матрицы А в порядке убывания. Алгоритм сортировки элементов матрицы для этого случая приведен на рис. 23.

Рис.22

Рис.23