Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сведения из теории. Цепь, состоящую из последовательно соединенных резистора (R), конденсатора (С) и индуктивности (L), называют колебательным контуром (рис

Цепь, состоящую из последовательно соединенных резистора (R), конденсатора (С ) и индуктивности (L), называют колебательным контуром (рис. 10.1).

Периодический процесс преобра­зо­ва­ния энергии электрического поля заряженного конденсатора в энергию магнитного поля катушки индуктивности и обратно называют электромагнитными колебаниями. Свободные электромагнитные колебания в любом ре­аль­ном контуре всегда затухающие. Пер­во­на­чальный запас энергии контура в процессе колебаний расходуется на нагревание проводов, по которым течет ток.

Запишем второй закон Кирхгофа для данного контура

.

Разделив это уравнение на L и заменив , а , получим

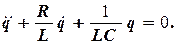(10.1)

Обозначим 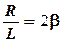, 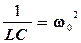. С учетом этих обозначений уравнение (10.1) примет вид

. (10.2)

Решением этого дифференциального уравнения является функция (при условии, что b < w ₀)

q = q _o e^{- b t} cos ( w t + a ). (10.3)

Из решения следует, что заряд на пластинах конденсатора меняется по гармоническому закону. Амплитуда колебаний со временем убывает по экспоненте.

Циклическая частота колебаний

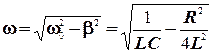. (10.4)

Нетрудно показать, что напряжение на пластинах конденсатора и ток в контуре меняются по гармоническому закону, аналогичному (10.3).

Период колебаний

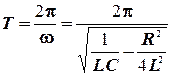. (10.5)

Если b (его называют коэффициентом затухания) много меньше w₀, то период колебаний определяется по формуле Томсона

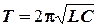. (10.6)