Порядок выполнения работы. 1. Оценить погрешность, которую дает соленоид конечных размеров, при определении вектора по сравнению с бесконечным соленоидом.

1. Оценить погрешность, которую дает соленоид конечных размеров, при определении вектора 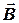по сравнению с бесконечным соленоидом.

Поле бесконечного соленоида однородно. В данной работе все теоретические формулы базируются на предположении, что магнитное поле создается бесконечно длинным соленоидом, т.е. индукция магнитного поля определяется выражением (8.5). Рабочий же соленоид имеет конечные размеры, следовательно, реальная индукция магнитного поля будет другая. Поэтому между теоретическими и экспериментальными результатами для e _i будет некоторое расхождение, оценить которое можно следующим образом

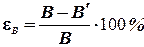. (8.13)

Подставив в выражение (8.13) формулы (8.5) и (8.6), получим

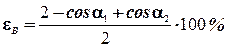. (8.14)

Зависимость между e_i и В линейная, поэтому расхождение при определении теоретического и экспериментального значений ЭДС не должно превышать расхождения для В.

По известным параметрам l и d (см. рис. 8.1) определим соs a₁ и сosa₂ не менее чем для двух точек, находящихся на оси соленоида в центральной его части.

Используя выражение (8.14), оценим расхождение для В в этих точках.

2. Теоретически и экспериментально определить ЭДС индукции в катушках.

Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer

Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.

Что умеет делать SeoHammer

— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.

SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.

Зарегистрироваться и Начать продвижение

2.1. Собрать схему (рис.8.4).

2.2. Подать напряжение с блока питания на соленоид. Частота подаваемого напряжения определяется по указанию преподавателя. По миллиамперметру определить величину тока I _д.

2.3. Поочередно подключая милливольтметр к выводам катушек, определить ЭДС, возникающую в них. Результаты занести в табл. 8.2 в строку e _iэ.

2.4. Используя выра­же­ние (8.12), вычислить теоре­ти­чес­кое значение e _iТ в каж­дой ка­­тушке при I _д и w, оп­ре­де­лен­­ных в п.2.

2.5. Оценить расхож­де­ние, полученное при тео­ре­ти­чес­ком и экспериментальном определении ЭДС. Сравнить его с тем, которое было получено в п. 1, и сделать вывод.

3. Определить зависимость e _i = f (s), где s -площадь катушки.

3.1. Используя экспериментальные данные, полученные в п. 2, вычислить ЭДС, возникающую в одном витке каждой катушки.

3.2. Построить график зависимости e _i = f (s).

4. Определить сдвиг фаз между током, текущим по соленоиду, и ЭДС индукции, возникающей в любой из катушек.

Выше было показано, что, если сила тока в соленоиде меняется по закону I = I ₀ сos w t, то

.

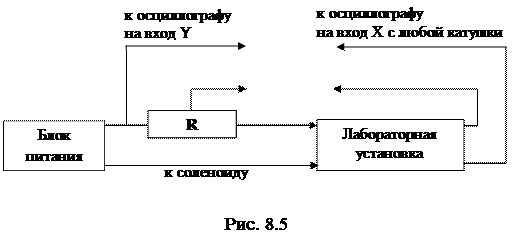
Это означает, что между током в соленоиде и ЭДС индукции в катушке существует сдвиг фаз. Для определения этого сдвига фаз воспользуемся осциллографом. Собрать схему (рис. 8.5). По виду фигуры, полученной на осциллографе, определим сдвиг фаз между током и ЭДС индукции.

5. Экспериментально сравнить коэффициенты взаимоиндукции L₁₂ и L ₂₁.

5.1. Пропустить ток I = 0, 5А через катушку K₁. Измерить ЭДС, возникающую в катушке K₃.

Сервис онлайн-записи на собственном Telegram-боте

Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.

Для новых пользователей первый месяц бесплатно.

Зарегистрироваться в сервисе

5.2. Пропустить такой же ток через катушку K₃. Измерить ЭДС, возникающую в катушке K₁. Сравнить полученные результаты и сделать вывод относительно L₁₂ и L₂₁.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается явление электромагнитной индукции?

2. Что такое магнитный поток и как он вычисляется?

3. Что называется потокосцеплением?

4. Как определяется индукция магнитного поля для конечного и бесконечного соленоидов?

5. Что такое коэффициент взаимоиндукции?

6. Вывести формулу для ЭДС катушки, находящейся внутри бесконечного соленоида, по которому течет ток.

7. Что называется действующим значением тока и напряжения, и как они связаны с амплитудными значениями?

ЛАБОРАТОРНАЯ РАБОТА № 9