Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Для диамагнетинов μ<l, для парамагнетиков >1.

40. Закон полного тока для магнитного поля в веществе.

Этот закон является обобщением закона полного тока для магнитного поля в вакууме (стр. 4-10).

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов,, охватываемых этим контуром,, умноженной на магнитную постоянную:

.

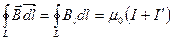где I и 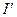— соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.

При этом циркуляция намагниченности 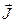по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, а циркуляция вектора 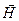— сумме токов проводимости, охватываемых этим контуром:

,

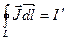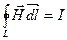
Последнее выражение представляет собой теорему о циркуляции вектора .

С учетом того, что сила тока I сквозь поверхность S, охватываемую контуром L, является потоком вектора плотности тока через эту поверхность, (стр.3-22), теорема о циркуляции вектора будет иметь вид:

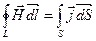
41. Условия на границе раздела двух магнетиков.

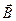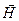Рассмотрим поведение векторов и на границе раздела двух однородных магнетиков с магнитными проницаемостям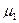и и 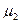при отсутствии на границе тока проводимости.

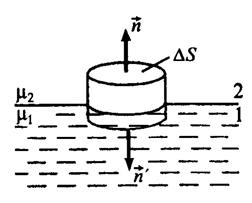
Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором.

Считаем, что основания Δ S цилиндра настолько малы, что в пределах каждого из них вектор 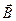неизменен. По теореме Гаусса

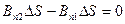
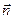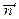(поскольку и противонаправлены). С учетом соотношения 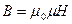, нормальные составляющие

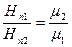
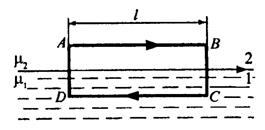
Вблизи границы раздела магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной l. Согласно теореме о циркуляции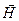

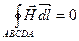
поскольку токов проводимости на границах нет. Отсюда

(знаки интегралов по АВ и CD разные. т.к. пути интегрирования противопо­ложны, а интегралы по ВС и DA бесконечно малы). Поэтому, тангенциальные составляющие

,

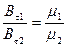
Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора 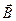и тангенциальная составляющая вектора 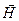изменяются непрерывно, а тангенциальная составляющая вектора 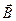и нормальная составляющая вектора 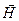претерпевают скачок.

42. Ферромагнетики и их свойства.

Помимо слабомагнитных веществ — диа- и парамагнетиков, существуют сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т.е. они сохраняют намагниченность при отсутствии внешнего магнитного поля.

В отличие от слабомагнитных веществ, у которых намагниченность J линейно изменяется с ростом Н, у ферромагнетиков, при увеличении Н, намагниченность растет сначала быстро, а затем выходит на насыщение .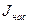

Магнитная проницаемость μ ферромаг­нетиков достигает больших значений (для железа — 5000, для сплава супермаллоя — 800 000).

Магнитная проницаемость и магнитная индукция В ферромагнетиков зависит от Н.

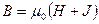в слабых полях растет быстро с ростом Н (участок 0-1-2 на рисунке {а)), а в сильных полях, поскольку 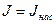, В растет с увеличением Н линейно (участок 2-3).

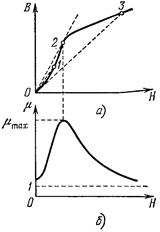
Соответственно 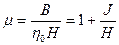вначале растет с ростом Н (рисунок (б)), а затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к единице.

Зависимость намагниченности / от напряженности магнитного поля Н в ферромагнетике определяется предысторией намагничения. Это явление называется магнитным гистерезисом. Если ферромагнетик намагнитить до насыщения (кривая 0-1), а затем уменьшать Н (кривая 1-2), то при Н = 0 в ферромагнетике останется остаточная намагниченность .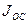

Это явление используют при изготовлении постоянных магнитов.

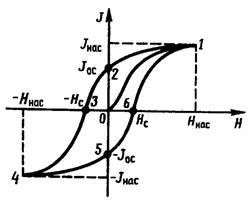
Для того чтобы уменьшить намагниченность до нуля, надо приложить противоположно-направленное поле (точка 3), с напряженностью 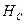, которая называется коэрцитивная сила. Придальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3-4), достигая насыщения (точка 4). Затем его можно опять размагнитить (кривая 4-5-6) и вновь перемагнитить до насыщения (кривая 6-1).

Таким образом, изменение намагниченности описывается кривой 1-2-3-4-5-6-1, которая называется петля гистерезиса.

Для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании выше точки Кюри ферромагнетик превращается в обычный парамагнетик.

Причина такого поведения в том, что при температурах ниже точки Кюри ферромагнетик разбивается на большое число микроскопических областей — доменов, самопроизвольно намагниченных до насыщения. Направление намагничения домена определенным образом связано с расположением атомов в ряды и слои (на рисунке схематически показаны домены в кристалле железа). При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенси­руют друг друга. Поэтому суммарный магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен.

Внешнее поле ориентирует по полю не магнитные моменты отдельных атомов (как это имеет место в случае парамагнетиков), а магнитные моменты целых областей спонтанной намагниченности, причем домены поворачиваются по полю скачком.

Формирование доменов обусловлено квантовыми свойствами электронов. Ферромагнитными свойствами обладают вещества, в атомах которых есть недостроенные внутренние электронные оболочки с нескомпернсированными спинами. В этом случае могут возникать обменные силы, которые вынуждают спиновые магнитные моменты электронов ориентироваться параллельно друг другу. Это приводит к возникновению областей спонтанного намагничения.

Существуют вещества, в которых обменные силы вызывают а нти параллельную ориентацию спиновых моментов электронов. Такие вещества называются антиферромагнетиками. Для них также существует антиферромагнитная точка Кюри (точка Нееля), выше которой разрушается магнитное упорядочение и антиферромагнетик превращается в парамагнетик.