На стадии синтеза

Наиболее распространенную продукцию, получаемую методом СВС-прессования, составляют пластины различной формы. Инициирование СВС в шихтовой заготовке производится локальным образом (в точке), и затем процесс протекает в режиме послойного горения. В известных работах по изучению теплового режима СВС-прессования и СВС-экструзии рассматривалась осесимметричная задача нестационарного теплообмена с движением фронта горения вдоль оси симметрии цилиндрической системы [57, 191, 192, 195]. При СВС-прессовании заготовка, имеющая форму круглой или квадратной пластины, размещена в цилиндрической пресс-форме перпендикулярно оси симметрии. Инициирование реакции горения производится с боковой поверхности или из центра шихтовой заготовки, и фронт горения движется перпендикулярно оси симметрии. В такой постановке исследования теплового режима не проводились.

Параметры теплового режима и размерность решаемой задачи зависят от координат точки инициирования реакции горения. При зажигании с боковой поверхности независимо от формы пластины теплообмен происходит в направлении трех пространственных координат. В случае инициирования реакции из центра квадратной пластины до момента выхода волны горения на боковую грань происходит осесимметричный, а затем трехмерный теплообмен. В круглой пластине при зажигании из центра в течение всего времени горения реализуется осесимметричный теплообмен. Технически более просто осуществить зажигание с боковой поверхности шихтовой заготовки, и этот вариант нашел наибольшее практическое применение.

Размерность температурного поля, сформировавшегося на стадии синтеза, определяет и размерность задачи пластического деформирования на стадии прессования. Решение трехмерных задач нестационарной теплопроводности и пластичности для системы нескольких тел является математически громоздким и трудоемким, поэтому в теоретических и прикладных исследованиях, как правило, ограничиваются рассмотрением плоских или осесимметричных математических моделей, которые позволяют достаточно полно выявить и исследовать основные закономерности физического процесса. Благодаря простоте конструкции формообразующего инструмента наиболее часто применяется СВС-прессование круглых заготовок в цилиндрической матрице, при котором происходит осесимметричное пластическое деформирование. Эта схема используется как в исследовательских целях при разработке рецептур новых материалов и экспериментальном изучении закономерностей уплотнения [50, 52, 102, 235], так и для выпуска продукции промышленного назначения [215]. С учетом вышеизложенного, в настоящей работе в качестве основного объекта исследования рассматривается СВС-прессование круглых пластин в цилиндрической матрице. Так как пластическое деформирование в этом случае является осесимметричным, то осесимметричным должно быть и температурное поле заготовок, поэтому для решения математически корректной задачи неизотермического осесимметричного пластического деформирования рассматривалось центральное зажигание. Вариант бокового зажигания рассматривался с целью изучения теплового режима реального процесса. Математическое моделирование и анализ процесса теплообмена при боковом зажигании впервые выполнены в работах [6, 202].

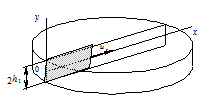
Решение трехмерной задачи нестационарного теплообмена в многослойной системе, которой соответствует вариант бокового зажигания, является математически громоздким и трудоемким. Для оценки компактируемости температурно-неоднородной заготовки достаточно иметь данные о температуре наиболее холодных областей. Такую информацию можно получить при рассмотрении двумерной модели теплообмена при горении плоского слоя единичной толщины с теплоизоляцией боковых граней. Слой вырезается таким образом, чтобы его длина была равна максимально возможному пути горения. Соответственно плоскости сечения проходят через точку зажигания и наиболее удаленную от нее точку. Такая модель позволяет описать поле температур в наиболее холодной (начало горения) и горячей (окончание горения) зонах заготовки. При боковом зажигании круглой заготовки сечение проходит по ее диаметру; при зажигании квадратной заготовки из центра боковой грани – через центр боковой грани и противоположную вершину квадрата (рис. 2.5). Чем дальше от горящего слоя находятся боковые поверхности заготовки, тем корректнее будет принятая модель. Отметим, что для плоской модели параметры расчетных зависимостей и получаемые результаты будут инвариантны к форме пластины.

Р и с. 2.5. Схема выделения плоского слоя при боковом зажигании

Физическая формулировка задачи заключается в следующем. Плоский слой единичной толщины высотой 2 h ₁ и длиной l помещен в песчаную оболочку и стальную матрицу также единичной толщины. Размеры оболочки и матрицы известны. В начальный момент времени на торце слоя инициируется реакция горения с известной температурой горения Т _г и скоростью горения u _г. Объект моделирования представляет собой плоскую трехэлементную систему с областями конечных размеров и с внутренней подвижной границей первого рода (фронт горения). Между элементами системы происходит нестационарный теплообмен. Теплообмен продуктов синтеза с оболочкой и оболочки с инструментом осуществляется при граничных условиях четвертого рода с идеальным тепловым контактом. На границе «инструмент - окружающая среда» имеют место граничные условия третьего рода. Теплообмен на боковых гранях слоя, оболочки и матрицы отсутствует. Фронт горения считается плоским и адиабатическим. Требуется найти температурное поле системы трех соприкасающихся тел в произвольный момент времени t.

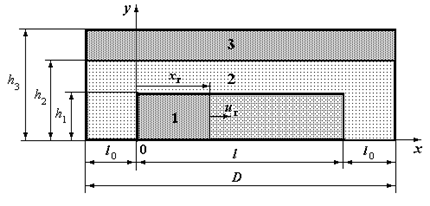
На рис. 2.6 приведена расчетная схема трехслойной системы, состоящей из плоского слоя длиной l, теплоизолирующей оболочки 2 и пуансона 3 диаметром D = l + 2× l _о мм. Горение слоя начинается с левой торцевой плоскости (x ₀ = 0); плоский фронт горения движется с постоянной скоростью u _г в направлении оси х. В силу осевой симметрии рассматривается половина высоты слоя в декартовых координатах х и у.

Р и с. 2.6. Расчетная схема объекта моделирования: 1 – продукты синтеза; 2 – оболочка; 3 – пуансон

Тепловой режим заготовок, имеющих форму пластин, формируется в основном за счет теплообмена на опорных поверхностях [144], поэтому в процессе теплообмена главную роль играет толщина оболочки между заготовкой и пуансоном или дном матрицы. Второстепенное значение имеют радиальные размеры оболочки между заготовкой и стенкой матрицы. С учетом изложенного в принятой модели рассматривается теплообмен между заготовкой и пуансоном (или дном матрицы) при варьировании толщины оболочки между ними. Толщина оболочки в радиальном направлении выбиралась из условия отсутствия сквозного прогрева оболочки и теплоотвода стенками матрицы. Как показали расчеты, для характерных временных параметров СВС-прессования сплавов системы ТiC-Ni полная теплоизоляция заготовки от боковых стенок матрицы обеспечивается при толщине оболочки l _о = 12 мм.

Математическая модель теплообмена на стадии горения
включает:

1) систему трех дифференциальных уравнений нестационарной теплопроводности в декартовых координатах

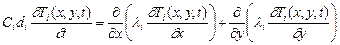; (2.15)

2) граничные условия:

на границах «заготовка-оболочка» (, ) и «оболочка-инструмент» (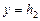) – условия IV рода

; ;

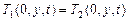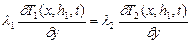; ; (2.16)

; ;

на границе «инструмент среда» (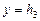) – условия III рода

l ₃ + a_т(T ₃- T _S) = 0; (2.17)

3) начальные условия

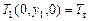; ; ; (2.18)

4) уравнение движения фронта горения

x _г = u _г × t; (2.19)

5) температуру подвижной границы I рода (фронт горения)

Т (х _г, y ₁, t) = Т _г; (2.20)

6) условие симметрии температурного поля относительно оси х

; (2.21)

7) условия адиабатичности перед фронтом горения (х = х _г+0)

(2.22, а)

и на наружных боковых поверхностях оболочки (х =- l _o и х = l + l _o)

; . (2.22, б)

При расчете температурного поля после сгорания всего слоя из системы уравнений (2.15)-(2.20) исключаются уравнения (2.18)-(2.20) и добавляются граничные условия четвертого рода на правой торцевой поверхности слоя при х = l:

l ₁ = l ₂ ; T ₁(l, y, t) = T ₂(l, у, t). (2.23)

В уравнениях (2.15)-(2.23) обозначено: Т_i – температура тел; С_i, d_i, l_i – удельная теплоемкость, гравиметрическая плотность и коэффициент теплопроводности тел системы; h_i – характерные размеры тел (см. рис. 2.6); i – индекс тела системы: 1 – продукты синтеза, 2 – оболочка, 3 – пуансон; t – время; х _г – текущая координата фронта горения; a _т – коэффициент теплоотдачи; Т_S – температура среды; n – нормаль к граничной поверхности.

Поставленная задача нестационарного теплообмена может быть решена только численным методом. В первой главе отмечалось, что среди численных методов решения краевых задач математической физики наиболее эффективным является метод конечных элементов (МКЭ). Теория и практическое применение МКЭ к различным задачам теплофизики и механики деформируемых твердых тел подробно изложены в обширной научной литературе [53, 65, 123, 130, 152, 171, 196, 227]. При решении задач механики деформируемых твердых тел рассматривается вариационная интерпретация МКЭ. Не все задачи тепломассопереноса допускают свое представление в вариационной форме, и для этого класса задач используется формулировка Галеркина [217]. В нашем случае нестационарные уравнения теплопроводности (2.14) с граничными условиями (2.15), (2.16) допускают вариационную формулировку, и им можно поставить в соответствие функционал Дьярмати следующего вида [48]:

, (2.24)

где V_i – объемы тел системы; S ₃ – площадь инструмента с конвективным теплообменом. Отличительной особенностью функционала (2.24) является то, что на стадии горения объем V ₁ горячих продуктов синтеза, с которыми происходит теплообмен, является функцией времени:

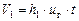. (2.25)

Процедура вычисления функционала (2.24) для температурного поля конечно-элементной области подробно рассмотрена в [171] и других работах. Согласно [171] условие минимизации функционала (2.24) приводит к следующему дискретному дифференциальному уравнению в матричной форме:

[ C ] +[L]× { T }={ F }. (2.26)

Здесь [ C ] – матрица теплоемкости; [L] – матрица теплопроводности; { T } – вектор-столбец узловых температур; { F } – вектор тепловых нагрузок. Если теплофизические свойства не зависят от температуры, то уравнение (2.26) является линейным. Линейное дифференциальное уравнение (2.26) решают методом конечных разностей [171], заменяя частную производную по времени ее конечно-разностным аналогом. На двухточечном шаблоне временные аппроксимирующие схемы в этом случае можно представить в форме

([ C ]+c× D t× [L])× { T_t } = ([ C ]-(1 - c)× D t [L])× { T ₀}+c× D t× { F_t }+

+(1 - c)× D t × { F ₀}, (2.27)

где c – параметр, влияющий на точность и устойчивость решения, причем его значения находятся в пределах 0 £ c £ 1. В уравнении (2.27) индексом t помечены неизвестные текущие, а индексом 0 – начальные значения параметров, которые полагаются известными. При c = 0 имеем явную разностную схему ² вперед², при c = 0, 5 – неявную центральную схему, при c = 1 – неявную разностную схему ² назад². Абсолютной устойчивостью обладают схемы, для которых
c³ 0, 5. Известны различные рекомендации по выбору величины коэффициента c [63, 125, 155]. В работе [125] методом конечных элементов исследован процесс электронагрева порошковой смеси, который носит взрывной характер и отличается высокими температурными градиентами. Установлено, что хорошее приближение к реальному физическому процессу дает неявная разностная схема ² назад² с c = 1. Теплообмен разогретых до температур свыше 2000 ^оС продуктов синтеза с оболочкой, имеющей комнатную температуру, также характеризуется высокими градиентами температуры, поэтому, как и в [125], в настоящей работе использовалась неявная разностная схема ² назад² при c = 1. В этом случае рекуррентная последовательность стационарных задач на каждом временном шаге D t имеет вид

([ C ] +D t × [L])× { T_k } = [ C ]× { T_{k -1}} +D t × { F_k }, (2.28)

где { T_{k -1}}, { T_k } – матрицы узловых значений температуры в начале и конце временного интервала D t.

Важным моментом математического моделирования является выбор физического приближения процесса. Для модели нестационарной теплопроводности принципиальным является вопрос о том, как влияют зависящие от температуры коэффициенты на температурное поле объекта. При учете зависимости теплофизических свойств продуктов СВС от температуры дифференциальное матричное уравнение (2.26) становится нелинейным. Соответственно на каждом интервале D t необходимо решать систему нелинейных алгебраических уравнений (2.28). При решении нелинейной задачи использовалась трехслойная разностная схема [64], которая приводит к следующему линейному матричному уравнению:

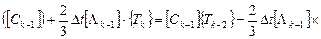
. (2.29)

В (2.29) зависящие от температуры матричные коэффициенты 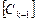и 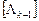определяются по распределению температуры в момент времени t_{k- 1}, соответствующий середине удвоенного интервала времени 2D t = t_k - t_{k- 2}. На первом временном шаге, когда температура неизвестна, решение находилось по уравнению (2.28).

Для дискретизации объекта использовались плоские треугольные элементы и линейная аппроксимация температуры внутри элемента [171]. При разбиении на конечные элементы вся область сначала покрывалась прямоугольной сеткой, а затем полученные прямоугольники диагоналями делились на два треугольника. В областях границ контактного теплообмена заготовки и оболочки с высокими градиентами температуры выполнялось сгущение сетки КЭ. Элементы матриц теплопроводности [L], теплоемкости [ C ] и вектора тепловых нагрузок { F_k } вычисляли по известным зависимостям для плоских треугольных элементов [171].

Имитация движения фронта горения производилась путем пошагового увеличения числа конечных элементов заготовки, участвующих в теплообмене. При прямоугольной конечно-элементной сетке вся область представляет собой набор вертикальных столбцов и горизонтальных слоев. В приближении плоского фронта горения за один шаг объем синтезированного материала увеличивается на объем элементов одного столбца заготовки. На 1-м шаге в теплообмене участвуют только элементы 1-го столбца заготовки шириной D х ₁. На 2-м шаге фронт горения перемещается на ширину элементов 2-го столбца заготовки D х ₂; на 3-м шаге – на ширину элементов 3-го столбца заготовки D х ₃ и т.д. На k -тoм шаге время горения t _{г k} нового столбца заготовки шириной D х_k составляет

. (2.30)

В течение этого времени происходит и охлаждение синтезированного объема заготовки. На каждом k -том шаге горения неизвестной является начальная контактная температура Т _к0 вновь образовавшейся поверхности контакта заготовки и оболочки, поэтому сначала по уравнениям (2.28), (2.29) при D t = 10^-6 с рассчитывается температура Т _к0 нового контактного узла, а затем эти уравнения решаются с шагом D t_k и определяется температурное поле в текущий момент времени. Для решения системы линейных уравнений (2.28) и (2.29) использовался итерационный метод Зейделя с точностью вычисления температуры 0, 5 ^оС.

Одной из основных задач при использовании численных методов является проблема соответствия результатов расчета точному решению краевой задачи. Сходимость численного решения к аналитическому достигается путем выбора размеров элементов сетки дискретной модели. При исследовании на сходимость необходимо иметь числовые результаты точного решения краевой задачи. Для рассматриваемой задачи нестационарного теплообмена с подвижной внутренней границей первого рода для тел конечных размеров такой информации нет, поэтому для определения оптимальных шагов по временной оси и пространственным координатам сопоставлялись численное и аналитическое решения одномерной задачи об охлаждении бесконечного слоя вещества в неограниченной среде при граничных условиях четвертого рода [111]. Установлено, что расхождение в 1% получается при толщине контактного слоя оболочки 0, 25 мм. Толщина двух следующих слоев составляет 0, 75 и 2 мм. В заготовке толщина трех первых слоев, начиная с контактного слоя, соответственно равна 0, 5; 1, 5 и 2 мм. Величина временного шага t _{г k}, рассчитанная по (2.30), должна быть не более (0, 1–0, 2) с. Указанные значения пространственно-временных координат и размеры заготовки с оболочкой определяют общее число узлов и элементов дискретной модели и, как следствие, порядок системы линейных уравнений (2.28), (2.29). При решении данной задачи общее число узлов составляло Nu = 351; число элементов Ne = 624.