Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Динамические структуры данных: двоичные деревья поиска
|
|
Дерево — это совокупность элементов, называемых узлами (при этом один из них определен как корень), и отношений (родительский–дочерний), образующих иерархическую структуру узлов. Узлы могут являться величинами любого простого или структурированного типа, за исключением файлового. Узлы, которые не имеют ни одного последующего узла, называются листьями.
В двоичном (бинарном) дереве каждый узел может быть связан не более чем двумя другими узлами. Рекурсивно двоичное дерево определяется так: двоичное дерево бывает либо пустым (не содержит ни одного узла), либо содержит узел, называемый корнем, а также два независимых поддерева — левое поддерево и правое поддерево.
Двоичное дерево поиска может быть либо пустым, либо оно обладает таким свойством, что корневой элемент имеет большее значение узла, чем любой элемент в левом поддереве, и меньшее или равное, чем элементы в правом поддереве. Указанное свойство называется характеристическим свойством двоичного дерева поиска и выполняется для любого узла такого дерева, включая корень. Далее будем рассматривать только двоичные деревья поиска. Такое название двоичные деревья поиска получили по той причине, что скорость поиска в них примерно такая же, что и в отсортированных массивах: O (n) = C • log2 n (в худшем случае O (n) = n).
Пример. Для набора данных 9, 44, 0, –7, 10, 6, –12, 45 построить двоичное дерево поиска.
Согласно определению двоичного дерева поиска число 9 помещаем в корень, все значения, меньшие его — на левое поддерево, большие или равные — на правое. В каждом поддереве очередной элемент можно рассматривать как корень и действовать по тому же алгоритму. В итоге получаем
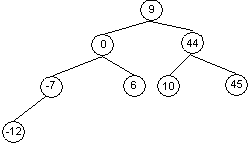
Выделим типовые операции над двоичными деревьями поиска:
· добавление элемента в дерево;
· удаление элемента из дерева;
· обход дерева (для печати элементов и т.д.);
· поиск в дереве.
Поскольку определение двоичного дерева рекурсивно, то все указанные типовые операции могут быть реализованы в виде рекурсивных подпрограмм (на практике именно такой вариант чаще всего и применяется). Отметим лишь, что использование рекурсии замедляет работу программы и расходует лишнюю память при её выполнении.
Пусть двоичное дерево поиска описывается следующим типом
Type BT=LongInt; U = ^BinTree; BinTree = Record Inf: BT; L, R: U End;
Покажем два варианта добавления элемента в дерево: итеративный и рекурсивный.
{Итеративный вариант добавления элемента в дерево, Turbo Pascal}
Procedure InsIteration(Var T: U; X: BT);
Var vsp, A: U;
Begin
New(A); A^.Inf: = X; A^.L: =Nil; A^.R: = Nil;
If T=Nil Then T: =A
Else Begin vsp: = T;
While vsp < > Nil Do
If A^.Inf < vsp^.Inf
Then
If vsp^.L=Nil Then Begin vsp^.L: =A; vsp: =A^.L End Else vsp: =vsp^.L
Else
If vsp^.R = Nil Then Begin vsp^.R: = A; vsp: =A^.R End Else vsp: = vsp^.R;
End
End;
{Рекурсивный вариант добавления элемента в дерево, Turbo Pascal}
Procedure InsRec(Var Tree: U; x: BT);
Begin
If Tree = Nil
Then Begin
New(Tree);
Tree^.L: = Nil;
Tree^.R: = Nil;
Tree^.Inf: = x
End
Else If x < Tree^.inf
Then InsRec(Tree^.L, x)
Else InsRec(Tree^.R, x)
End;
Аналогично на C++.
typedef long BT;
struct BinTree{
BT inf;
BinTree *L; BinTree *R;
};
/* Итеративный вариант добавления элемента в дерево, C++ */
BinTree* InsIteration(BinTree *T, BT x)
{ BinTree *vsp, *A;
A = (BinTree *) malloc(sizeof(BinTree));
A-> inf=x; A-> L=0; A-> R=0;
if (! T) T=A;
else {vsp = T;
while (vsp)
{if (A-> inf < vsp-> inf)
if (! vsp-> L) {vsp-> L=A; vsp=A-> L; }
else vsp=vsp-> L;
else
if (! vsp-> R) {vsp-> R=A; vsp=A-> R; }
else vsp=vsp-> R;
}
}
return T;
}
/* Рекурсивный вариант добавления элемента в дерево, C++ */
BinTree* InsRec(BinTree *Tree, BT x)
{
if (! Tree) {Tree = (BinTree *) malloc(sizeof(BinTree));
Tree-> inf=x; Tree-> L=0; Tree-> R=0;
}
else if (x < Tree-> inf) Tree-> L=InsRec(Tree-> L, x);
else Tree-> R=InsRec(Tree-> R, x);
return Tree;
}
Существует несколько способов обхода (прохождения) всех узлов дерева. Три наиболее часто используемых из них называются обход в прямом (префиксном) порядке, обход в обратном (постфиксном) порядке и обход во внутреннем порядке (или симметричный обход). Каждый из обходов реализуется с использованием рекурсии.
Ниже приведены подпрограммы печати элементов дерева с использованием обхода двоичного дерева поиска в обратном порядке.
{Turbo Pascal}
Procedure PrintTree(T: U);
begin
if T < > Nil
then begin PrintTree(T^.L); write(T^.inf: 6); PrintTree(T^.R) end;
end;
// C++
void PrintTree(BinTree *T)
{
if (T) {PrintTree(T-> L); cout < < T-> inf< < " "; PrintTree(T-> R); }
}
Реализуем функцию, возвращающую true (1), если элемент присутствует в дереве, и false (0) — в противном случае.
{Turbo Pascal}
function find(Tree: U; x: BT): boolean;
begin
if Tree=nil then find: = false
else if Tree^.inf=x then Find: = True
else if x < Tree^.inf
then Find: = Find(Tree^.L, x)
else Find: = Find(Tree^.R, x)
end;
/* C++ */
int Find(BinTree *Tree, BT x)
{ if (! Tree) return 0;
else if (Tree-> inf==x) return 1;
else if (x < Tree-> inf) return Find(Tree-> L, x);
else return Find(Tree-> R, x);
}
По сравнению с предыдущими задача удаления узла из дерева реализуется несколько сложнее. Можно выделить два случая удаления элемента x (случай отсутствия элемента в дереве является вырожденным):
1) узел, содержащий элемент x, имеет степень не более 1 (степень узла — число поддеревьев, выходящих из этого узла);
2) узел, содержащий элемент x, имеет степень 2.
Случай 1 не представляет сложности. Предыдущий узел соединяется либо с единственным поддеревом удаляемого узла (если степень удаляемого узла равна 1), либо не будет иметь поддерева совсем (если степень узла равна 0).
Намного сложнее, если удаляемый узел имеет два поддерева. В этом случае нужно заменить удаляемый элемент самым правым элементом из его левого поддерева.
{Turbo Pascal}
function Delete(Tree: U; x: BT): U;
var P, v: U;
begin
if (Tree=nil)
then writeln('такого элемента в дереве нет! ')
else if x < Tree^.inf then Tree^.L: = Delete(Tree^.L, x) {случай 1}
else
if x > Tree^.inf
then Tree^.R: = Delete(Tree^.R, x) {случай 1}
else
begin {случай 1}
P: = Tree;
if Tree^.R=nil
then Tree: =Tree^.L
else if Tree^.L=nil
then Tree: =Tree^.R
else begin
v: = Tree^.L;
if v^.R < > nil
then begin
while v^.R^.R < > nil do v: = v^.R;
Tree^.inf: = v^.R^.inf;
P: = v^.R;
v^.R: =v^.R^.L;
end
else begin Tree^.inf: = v^.inf;
P: = v;
Tree^.L: = Tree^.L^.L
end
end;
dispose(P);
end;
Delete: = Tree
end;
{C++}
BinTree * Delete(BinTree *Tree, BT x)
{ BinTree* P, *v;
if (! Tree) cout < < " такого элемента в дереве нет! " < < endl;
else if (x < Tree-> inf) Tree-> L = Delete(Tree-> L, x);
else if (x > Tree-> inf) Tree-> R = Delete(Tree-> R, x);
else {P = Tree;
if (! Tree-> R) Tree = Tree-> L; // случай 1
else if (! Tree-> L) Tree = Tree-> R; // случай 1
else // случай 2
{ v = Tree-> L;
if (v-> R)
{
while (v-> R-> R) v = v-> R;
Tree-> inf = v-> R-> inf;
P = v-> R; v-> R = v-> R-> L;
}
else
{
Tree-> inf = v-> inf;
P = v;
Tree-> L=Tree-> L-> L;
}
}
free(P);
}
return Tree;
}
Примечание. Если элемент повторяется в дереве несколько раз, то удаляется только первое его вхождение.
Разработаем процедуру создания двоичного дерева поиска, содержащего n элементов.
{Turbo Pascal}
procedure sozd(var Tree: U);
var i, n: integer; a: bt;
begin
Tree: = nil;
write('Сколько элементов? '); readln(n);
for i: =1 to n do
begin
write('Введите очередной элемент: ');
readln(a);
Insrec(Tree, a)
end
end;
Контрольные вопросы и задания
1. Что такое рекурсивный алгоритм?
2. Из каких частей строится определение рекурсивного алгоритма?
3. Что является обязательным в любом рекурсивном алгоритме?
4. Можно ли рекурсию заменить итерацией? Можно ли итерацию заменить рекурсией?
5. Каков принцип построения динамической структуры «дерево»?
6. Перечислите сходства и отличия динамических структур типа «линейный список», «стек», «дерево».
7. Перечислите структуры, которые можно представить в виде дерева, которые встречаются в повседневной жизни.
8. Закончите фразу: «Линейный список — это дерево, в котором …».
9. Реализуйте итеративные варианты тех алгоритмов обработки дерева, которые представлены в рекурсивной форме.
10. Написать рекурсивную процедуру, которая печатает элементы из всех листьев дерева.
11. Написать рекурсивную функцию, которая определяет глубину заданного элемента на дереве и возвращает –1, если такого элемента нет.
12. Написать процедуру, которая печатает (по одному разу) все вершины дерева.
13. Написать процедуру, которая по заданному n считает число всех вершин глубины n в заданном дереве.
14. Написать процедуру, которая определяет глубину дерева.
|
|