Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Циркуляция вектора магнитной индукции

Ранее мы вводили понятие циркуляции вектора напряженности электростатического поля (см. (4.5)) по замкнутому контуру L:

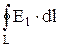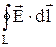= = 0.

Из равенства нулю циркуляции вектора электростатического поля вдоль любого замкнутого контура следует, что электростатическое поле потенциальное.

Аналогичное понятие можно ввести для вектора магнитной индукции . Циркуляцией вектора в вакууме по заданному замкнутому контуру называется интеграл:

= ,

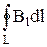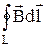где 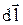- вектор элементарной длины контура, направленной вдоль направления обхода контура, B_l = Bcosa - проекция вектора на направление контура (с учетом выбранного направления обхода), a - угол между векторами и .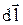

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ) – циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром:

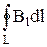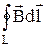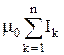= = , (36.1)

где n - число проводников с токами, охватываемых контуром L произвольной формы.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.

Из того, что циркуляция вектора отлична от нуля, следует, что магнитное поле является вихревым, т.е. силовые линии вектора имеют вид замкнутых кривых.

Выражение (36.1) справедливо только для поля в вакууме, так как для поля в веществе необходимо учитывать молекулярные токи.

Теорема о циркуляции вектора имеет в учении о магнитном поле такое же значение, как и теорема Остроградского-Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био-Савара-Лапласа.

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида, находящегося в вакууме. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток I (рисунок 45). Длину соленоида считаем во много раз больше, чем диаметр его витков, т.е. рассматриваемый соленоид можно считать бесконечно длинным. Экспериментальное изучение магнитного поля длинного соленоида показывает, что внутри соленоида поле является однородным, вне соленоида - неоднородным и очень слабым.

На рисунке 45 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур 12341, как показано на рисунке 45. Циркуляция вектора по замкнутому контуру 12341, охватывающему все N витков, согласно (36.1), равна

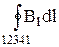= m₀NI. (36.2)

Интеграл (36.2) по прямоугольному контуру 12341 можно представить в виде четырех слагаемых по отрезкам 12, 23, 34 и 41. На участках 12 и 34 контур перпендикулярен линиям магнитной индукции и B_l = 0. На участке 23 вне соленоида В = 0. На участке 41 циркуляция вектора равна Bl (контур совпадает с линией магнитной индукции). Следовательно,

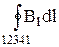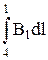= = Bl = m₀NI. (36.3)

Из (36.3) приходим к выражению для магнитной индукции поля внутри соленоида в вакууме:

В = m₀ 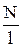I. (36.4)

Отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био-Савара-Лапласа; в результате получается та же формула (36.4).

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора ) является обобщением закона (36.1):

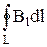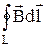= = m₀(I+I¢), (36.5)

где I и I¢ - соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.

Таким образом, циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор , таким образом, характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции не имеют источников и являются замкнутыми.

Можно доказать, что циркуляция намагниченности 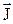по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

= I¢. (36.6)

Тогда закон полного тока для магнитного поля в веществе можно записать также в виде

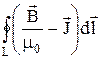= I, (36.7)

где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (36.7), согласно (34.7), есть не что иное, как введенный ранее вектор 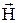напряженности магнитного поля:

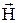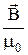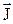= - . (36.8)

Итак, циркуляция вектора 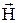по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:

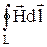= I. (36.9)

Выражение (36.8) представляет собой теорему о циркуляции вектора .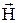

Как видно из (36.8) вектор 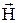представляет собой комбинацию двух различных величин /m₀ и 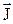. Поэтому вектор 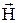- вспомогательный вектор, не имеющий физического смысла. Однако во многих случаях его использование значительно упрощает изучение поля в магнетиках.